标签:root ++ minimum empty ini 设置 输入 ring 前序遍历
二叉查找树(二叉搜索树):
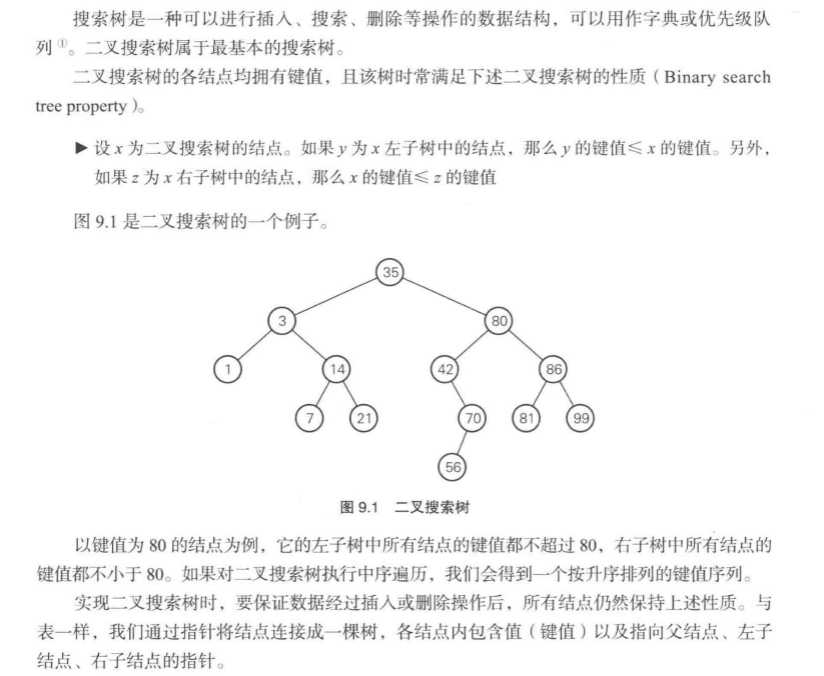
——摘自《挑战》
输入若干条命令,执行以下操作:
insert x——将x插入到二叉排序查找树中
delete x——从二叉排序查找树中删除x
find x——从二叉排序查找树中查找x,找到则输出yes,否则输出no
min——输出该二叉排序查找树的最小值
traverse——输出中序遍历该二叉树的结果
pre——输出先序遍历该二叉树的结果
post——输出后序遍历该二叉树的结果
level——输出层序遍历该二叉树的结果
Code:
1 #include<bits/stdc++.h> 2 using namespace std; 3 struct Node //二叉搜索树的结点 4 { 5 int key; 6 Node *left,*right,*parent; 7 }; 8 Node *root,*NIL; 9 void insert(int k)//插入操作 10 { 11 Node *y=NIL; //x的父结点 12 Node *x=root; 13 Node *z; 14 15 z=(Node *)malloc(sizeof(Node)); 16 z->key=k; 17 z->left=NIL; 18 z->right=NIL; 19 20 while(x!=NIL){ 21 y=x; //设置父结点 22 if(z->key<x->key) 23 x=x->left; //移动至左结点 24 else 25 x=x->right; //移动至右结点 26 } 27 z->parent=y; 28 29 if(y==NIL) 30 root=z; 31 else{ 32 if(z->key<y->key) 33 y->left=z; 34 else 35 y->right=z; 36 } 37 } 38 Node *find(Node *root,int k)//查找操作 39 { 40 while(root!=NIL&&k!=root->key){ 41 if(k<root->key) 42 root=root->left; 43 else 44 root=root->right; 45 } 46 return root; 47 } 48 Node *treeMinimum(Node *x)//二叉搜索树的最小值 49 { 50 while(x->left!=NIL) 51 x=x->left; 52 return x; 53 } 54 Node *treeSuccessor(Node *x)//搜索后一个结点 55 { 56 if(x->right!=NIL) 57 return treeMinimum(x->right); 58 Node *y=x->parent; 59 while(y!=NIL&&x==y->right){ 60 x=y; 61 y=y->parent; 62 } 63 return y; 64 } 65 void treeDelete(Node *z)//删除操作 66 { 67 Node *y; //要删除的对象 68 Node *x; //y的子节点 69 70 //确定要删除的结点 71 if(z->left==NIL||z->right==NIL)//z没有或只有一个子结点时,要删除的对象为z 72 y=z; 73 else //z有两个子结点时,删除对象为z的后一个结点 74 y=treeSuccessor(z); 75 //确定y的子结点x 76 if(y->left!=NIL)//如果y有左子结点,则x为y的左子结点 77 x=y->left; 78 else //如果y没有左子结点,则x为y的右子结点 79 x=y->right; 80 81 if(x!=NIL) 82 x->parent=y->parent;//设置x的父结点 83 84 if(y->parent==NIL)//如果y是根结点,则x成为树的根节点 85 root=x; 86 else{ 87 if(y==y->parent->left)//如果y是其父结点p的左子结点,则x成为p的左子结点 88 y->parent->left=x; 89 else //如果y是其父结点p的右子结点,则x成为p的右子结点 90 y->parent->right=x; 91 } 92 93 if(y!=z)//z的后一个结点被删除时 94 z->key=y->key; //将y的数据复制到z中 95 96 free(y); 97 } 98 void inorder(Node *root)//中序遍历 99 { 100 if(root==NIL)return; 101 inorder(root->left); 102 printf("%d ",root->key); 103 inorder(root->right); 104 } 105 void preorder(Node *root)//先序遍历 106 { 107 if(root){ 108 printf("%d ",root->key); 109 preorder(root->left); 110 preorder(root->right); 111 } 112 } 113 void postorder(Node *root)//后序遍历 114 { 115 if(root!=NULL){ 116 postorder(root->left); 117 postorder(root->right); 118 printf("%d ",root->key); 119 } 120 } 121 void levelorder(Node *root){ //层序遍历 122 if(root!=NULL){ 123 queue<Node*>que; 124 que.push(root); 125 Node *p; 126 while(!que.empty()){ 127 p=que.front(); 128 que.pop(); 129 printf("%d ",p->key); 130 if(p->left!=NULL) 131 que.push(p->left); 132 if(p->right!=NULL) 133 que.push(p->right); 134 } 135 } 136 } 137 int main() 138 { 139 string order; 140 int x; 141 while(!(cin>>order).eof()) //输入命令 142 { 143 if(order=="insert"){ //把x插入到二叉排序查找树中 144 scanf("%d",&x); 145 insert(x); 146 } 147 else if(order=="find"){ //查找x,找到则输出yes,否则输出no 148 scanf("%d",&x); 149 Node *t=find(root,x); 150 if(t!=NIL) 151 printf("yes\n"); 152 else 153 printf("no\n"); 154 } 155 else if(order=="delete"){ //从二叉排序查找树删除x 156 scanf("%d",&x); 157 treeDelete(find(root,x)); 158 } 159 else if(order=="min"){ //从二叉排序树中查找最小值输出 160 Node *MIN=treeMinimum(root); 161 printf("%d\n",MIN->key); 162 } 163 else if(order=="traverse"){ //输出中序遍历该二叉树的结果(升序排列序列) 164 inorder(root); 165 printf("\n"); 166 } 167 else if(order=="pre"){ //输出前序遍历 168 preorder(root); 169 printf("\n"); 170 } 171 else if(order=="level"){ //输出层序遍历 172 levelorder(root); 173 printf("\n"); 174 } 175 else if(order=="post"){ //输出后序遍历 176 postorder(root); 177 printf("\n"); 178 } 179 } 180 return 0; 181 }
运行结果:
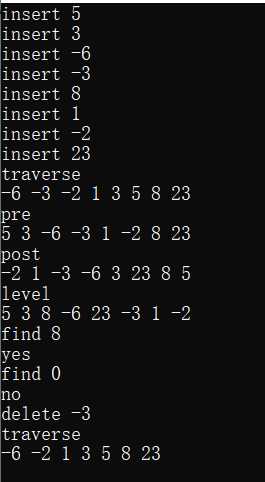
标签:root ++ minimum empty ini 设置 输入 ring 前序遍历
原文地址:https://www.cnblogs.com/HOLLAY/p/11331067.html