标签:oid swap void 角度 space target 解释 pre 顺序
首先安利自己倍增求LCA的博客,前置(算不上)知识在此。
LCA有3种求法:倍增求lca(上面qwq),树链剖分求lca(什么时候会了树链剖分再说。),还有,标题。
是的你也来和我一起学习这个了qwq。
开始吧。
众所周知,每当你dfs时,你都能产生一棵dfs树,可以根据你的dfs序来构建。
such as(丑陋的画风):
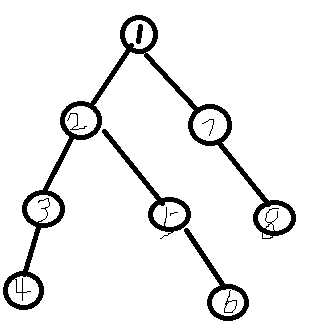
一个dfs的顺序。
以这个为例:
那么我们写出他的遍历顺序:
假如我们要求3,8(wtf?)的LCA,
那么我们首先写出他的bfs序:
123432565217871。
然后留意一下我们要求的两个数的位置。
123432565217871。
我们发现这样一个事情:
两个数的LCA,一定在前一个数最后一次出现的位置(在bfs序中)。
感性证明:
对于前一个数最后一次出现的位置,他的意义就是当前节点的子树已经遍历完了,并且正在进行回溯!(拍桌,划重点!)。
也就是说,他要回溯到他的祖先了,而它的祖先同样也是后一个节点的祖先,一定在后一个节点遍历前,前一个节点回溯后。
前一个节点<lca<后一个节点。
证毕。
那么,我们只要找到dfs遍历顺序中的 “前一个数最后一次出现的位置,后一个数第一次出现的位置”,这个区间取出区间最小值,即是两个节点的lca。
或许有人会说:为什么最小值一定是lca呢?
又需要证明了。
我们从几何学的角度来解释:
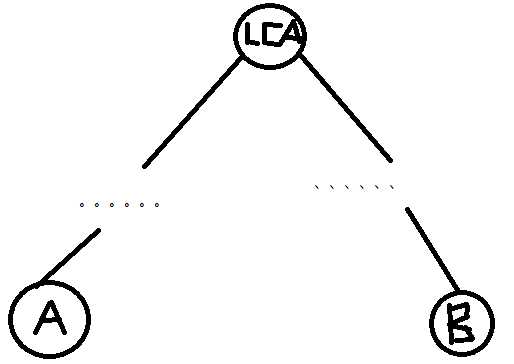
由图可知,两个节点分别在LCA的两个不同的子树中。
当A节点最后一次遍历完,经过一系列回溯,一定能回溯的LCA。
但是因为LCA的子树没有遍历完(链式存图i=edge[i].to),所以它只会遍历到LCA,然后继续遍历lca的子树直到遍历到B点。
感性证毕。
内么,区间最小值且不带修改的我们很容易想到st表。
所以,dfs序+RMQ求LCA成立。
复杂度nlogn查询+o1查询,三者最优。
代码:
#include<bits/stdc++.h> using namespace std; const int M = 1e5 + 10 ; vector<int> g[M] ; int n ; vector<int> vs ;//dfs order int tot ; int orm[M] ; int id[M] ; int dep[M] ; int d[M][30] ;//RMQ void dfs (int o , int u ,int DEP) { int tmp = tot ++ ; dep[u] = DEP ; id[u] = vs.size () ; orm[tmp] = u ; vs.push_back (tmp) ; for (int i = 0 ; i < g[u].size () ; i ++) { int v = g[u][i] ; if (v == o) continue ; dfs (u , v , DEP + 1) ; } int len = vs.size () ; if (vs[len-1] == tmp) vs.push_back (vs[id[o]]) ; else vs.push_back (tmp) ; } void init_RMQ () { for (int i = 0 ; i < 2*n-1 ; i ++) d[i][0] = vs[i] ; for (int j = 1 ; (1 << j) <= n ; j ++) { for (int i = 0 ; i + (1 << j) <= n ; i ++) { d[i][j] = min (d[i][j-1] , d[i+(1<<(j-1))][j-1]) ; } } } int RMQ (int l , int r) { printf ("l = %d , r = %d\n" , l , r ) ; int k = 0 ; while ( (1<<(k+1)) <= r - l + 1) k ++ ; int tmp = min (d[l][k] , d[1+r-(1<<k)][k]) ; return orm[tmp] ; } void Print () { for (int i = 0 ; i < 2*n-1 ; i ++) printf ("%3d " , i ) ; puts ("") ; puts ("dfs order:") ; for (int i = 0 ; i < 2*n-1 ; i ++) printf ("%3d " , vs[i]) ; puts ("") ; puts ("deep:") ; for (int i = 0 ; i < n ; i ++) printf ("%3d " , dep[i]) ; puts ("") ; puts ("id :") ; for (int i = 0 ; i < n ; i ++) printf ("%3d " , id[i]) ; puts ("") ; } void LCA () { dfs (0,0,0) ; init_RMQ () ; Print () ; } int main () { cin >> n ; for (int i = 0 ; i < n - 1 ; i ++) { int u , v ; cin >> u >> v ; g[u].push_back (v) ; g[v].push_back (u) ; } LCA () ; int Q ; cin >> Q ; while (Q --) { int u , v ; cin >> u >> v ; if (id[u] > id[v]) swap (u , v ) ; int ans = RMQ (id[u] , id[v]) ; printf ("The %d and %d the lastest ans is %d , and they are away from %d\n" , u , v , ans , dep[u]+dep[v]-2*dep[ans]) ; } return 0 ; }
——lyfdalao
完结。
标签:oid swap void 角度 space target 解释 pre 顺序
原文地址:https://www.cnblogs.com/lbssxz/p/11332818.html