标签:最小割 span 最大匹配 起点 ora 个数 bsp image tarjan

说人话:
边双联通:
a到b的路径上无必经边
点双联通:
a到b的路径上除了a,b没有必经点
tarjan求点双联通:


代码(补图)
割点:

桥:
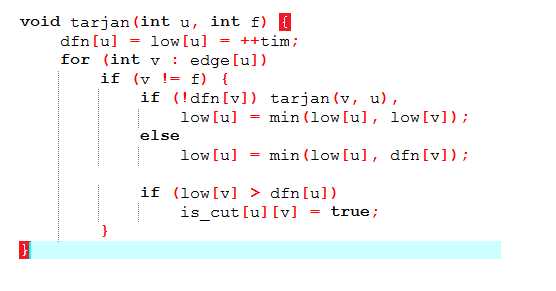
求点双:强制dfs时不越过割点,即可求出一个块
求边双:dfs时不越过桥

不是割点:减少2n-1
是割点:减少sigmai的大小*其他所有子树的大小

tarjan求桥,然后缩点,会形成一棵树。把树的所有叶子连起来用的边数就是答案
判断:

当且仅当无向图上不含奇环的时候就是二分图



增广路特点:非匹配边比匹配边多一条
寻找增广路:dfs
咕咕咕~
网络流:

最小割最大流定理:网络流的最大流就是整个图的最小割
dinic:类似匈牙利算法的思路,不断寻找当前最大流能加1的方案
直到不能再加
先dfs一遍,确定每个点到源点s的距离,
同时不断加边,维护当前流量
毒瘤操作:减少某条边的流量
所以就减反向边,边权为0,表示从终点到起点可扩充流量
二分图最大匹配怎么用网络流搞?
在左边建一个超级源点s,在右边建一个超级汇点t
s向每个左边的点建一个流量为1的边,右边的点向t建流量为1的边
二分图中间的点不停的寻找能加流量的路,能加就加,知道不能加
总之最大流就是最大匹配


二分图建图小技巧:
如果有x轴,y轴,且有一个坐标(x0,y0)
则就由x0向y0建一条边
国际象棋棋盘:黑白染色(黑的向白的建边)
就是最小覆盖qwq
因为消灭一行x0就是把x0那个点的所有连边都覆盖掉
消灭一列同理
所以打一次抢就相当于覆盖一撮边
最小顶点覆盖=最大匹配数

特别的,一个点也是一个路径
玄学转化二分图:

|v|是顶点个数
为什么上面说的是对的?
假设我们现在覆盖到了u,再从u选择一条出边,到了v,v就不用再来一条路径搞覆盖了。所以每多选一条边,答案就减1.
//图
但是每个点只能选出一条出边,一条入边。对于每个点,我们把它拆成两个,一个出点,一个入点。
所以就这么玄学的转化成了二分图
我们选的边在二分图上就是一个匹配
窝盟每选一条边,那么就有一个点不用再来一条路径进行覆盖了,也就是答案会在原来的基础上-1.所以我们要选出尽可能多的边来覆盖尽可能多的点,设覆盖的点最多为k,则答案就是n-k。
按照上述的转化方式,就是求转化后的二分图最大匹配 
建大约n2条边然后最小路径覆盖???
还真是啊.....
然后就搞完了
匈牙利算法说人话:
找到一个点v:v是非匹配点----->把这条边设为匹配边,再找非匹配边;
v是匹配点-------->走完这条匹配边,到了边的终点,然后再找非匹配边



今天莫得糖果,所以就分白砂糖好了,一人一堆慢慢数有几颗
裸的查分约束,少的向多的建边权为1的边
大于等于:边权为0,小的向大的建边
小于等于:边权为0,还是小的向大的建边
玄学建边方向判断:
现在有这样的一条边
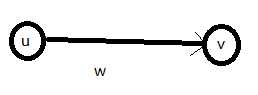
跑最短路
dis[v]<=dis[u]+w
跑最长路:
dis[v]>=dis[u]+w
根据选择跑的路推一推就知道谁想谁建边辣
出现等于:连大于等于,小于等于
最短or最长?
迷惑行为大赏
跑最长路
why?因为要考虑所有的约束条件啊
看一张丑陋的图就知道为什么了
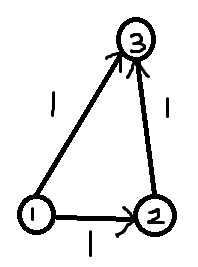
显然dis[3]是2不是1
出现正环就药丸

超级源点的d为0

ysq:论是账本伪造还是刁姹算错???
[l,r]的加起来=k,则xr-xl=k
我们可以处理出前缀和数组s[i],表示前i个数的和
这样就会有s[r]-s[l-1]=k的形式的约束条件
当然了这个前缀和数组也是充满了毒瘤
需要我们跑最短路维护
然后dfs找有没有负环

爆......爆搜?!
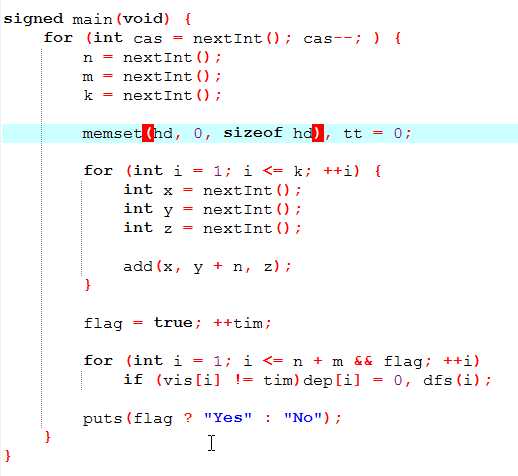
仍旧是按照二分图建图的duliu建法,每次就相当于在某一个点的所有出边的边权+1或-1,然后限制就是(x,y)这条边的边权是c
于是我们考虑爆搜(当出现冲突的时候说明无解)
标签:最小割 span 最大匹配 起点 ora 个数 bsp image tarjan
原文地址:https://www.cnblogs.com/lcez56jsy/p/11334312.html