标签:mes 最优二叉树 切割 log space 深度 hellip pop names
链接:http://poj.org/problem?id=3253
#include<iostream> #include<queue> #include<vector> using namespace std; typedef long long ll; const int MAX_L=5e4+50; int N; // N是木板切割块数 int L[MAX_L]; void solve(){ ll ans=0; //声明一个从小到大取出数值的优先队列 priority_queue<int,vector<int>,greater<int> > que; for(int i=0;i<N;++i){ que.push(L[i]); } //循环到只剩一块木板为止 while(que.size()>1){ //取出最短的木板和次短的木板 int l1,l2; l1=que.top(); que.pop(); l2=que.top(); que.pop(); //把两块木板合并 ans+= l1+l2; que.push(l1+l2); } printf("%lld\n",ans); } int main(){ scanf("%d",&N); for(int i=0;i<N;++i){ scanf("%d",&L[i]); } solve(); return 0; }
木板切割顺序不定,自由度很高,为了使开销尽可能地小,可采用最优二叉树的结构
首先,切割的方法可以参考下图的二叉树
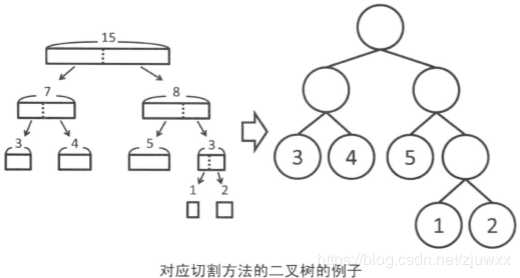
每个叶子节点对应一块切割的木板。叶子节点深度对应为得到木板所需的切割次数
开销就等于各叶子节点的 木板长度 * 节点深度 的总和。例如上图的开销就等于 3 * 2+4 * 2+5 * 2+1 * 3+2 * 3 = 33
此时最佳切割方法应具有如下性质:最短的板与次短的板的节点应当是兄弟节点
不妨将 Li 按由小到大的顺序排序,最短的板是 L1,次短的板是 L2。如果它们在二叉树中是兄弟节点,那么意味着它们是从一块长度为(L1 + L2)的木板上切割所得。由于切割顺序不定,不妨当作最后被切割,这样切割前就有 (L1 + L2)、L3、L4、…、Ln这样 N-1块木板存在,递归地对剩下 N-1块木板求解即可得出答案
优先队列可以实现对压入数据的排序,因此借用该结构可大大降低时间复杂度,由 O(N^2) 变成 O(N * logN)
标签:mes 最优二叉树 切割 log space 深度 hellip pop names
原文地址:https://www.cnblogs.com/E-mperor/p/11336217.html