标签：一个   ble   遍历   return   ace   problem   get   size   查找树   

---恢复内容开始---

简介

　　在计算机科学中，二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用作二叉查找树和二叉堆或是二叉排序树。

基本术语　

1. 子树：除了根节点外，每个子节点都可以分为多个不相交的子树。
2. 孩子与双亲：若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。
3. 兄弟：具有相同双亲的节点互为兄弟。
4. 节点的度：一个节点拥有子树的数目。
5. 叶子：没有子树，也即是度为0的节点。
6. 分支节点：除了叶子节点之外的节点，也即是度不为0的节点。
7. 内部节点：除了根节点之外的分支节点。
8. 层次：根节点为第一层，其余节点的层次等于其双亲节点的层次加1.
9. 树的高度：也称为树的深度，树中节点的最大层次。
10. 有序树：树中节点各子树之间的次序是重要的，不可以随意交换位置。
11. 无序树：树种节点各子树之间的次序是不重要的。可以随意交换位置。
12. 森林：0或多棵互不相交的树的集合。

基本形态

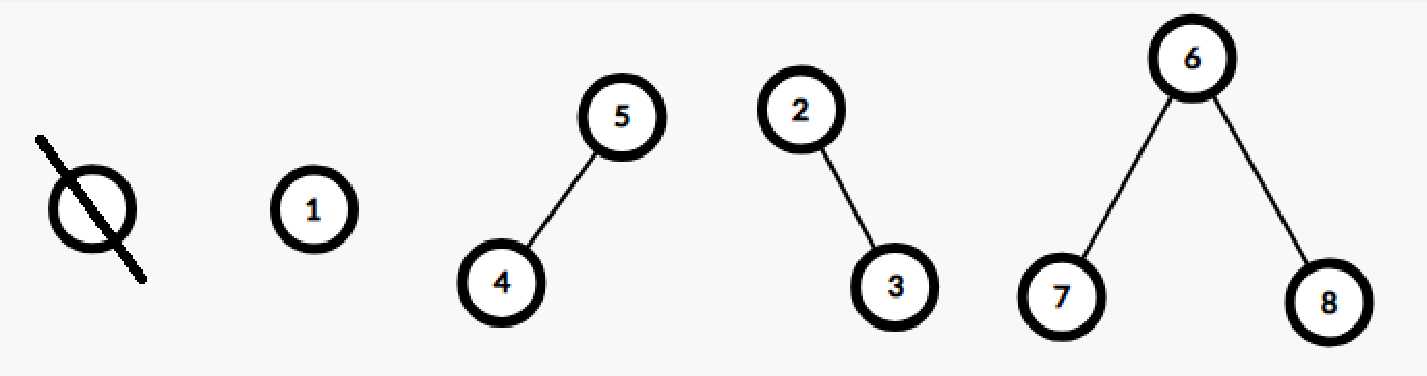
也就五种，从左往右分别是空树，只有根节点的树，根节点和左儿子，根节点和右孩子，根节点和左右孩子。

基本性质

1.二叉树第i层上的结点数目最多为2^i-1(i>=1)

2.深度为k的二叉树至多有2^k-1个结点（k>=1）

3.包含n个结点的二叉树的高度至少为(log₂n)+1

4.在任意二叉树中，若度为0的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

5.如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层开始到最下一层，每一层从左到右编号），对任一节点i有：

1. 如果i=1 ，则节点为根节点，没有双亲。
2. 如果2*i > n ，则节点i没有左孩子 ；否则其左孩子节点为2*i （n为节点总数）
3. 如果2*i+1>n ，则节点i没有右孩子；否则其右孩子节点为2*1+1

满二叉树

　　就像它的名字一样，它是满的（废话）

　　满二叉树是指一个高度为n的树有2^(n-1)个结点（其实就是每个点都有两个孩子，除了最后一层的单身狗）

完全二叉树

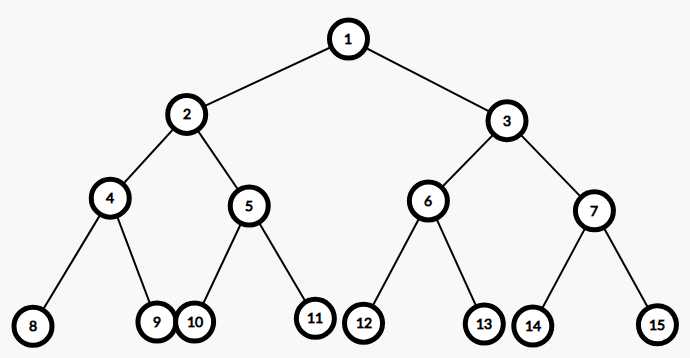
　　完全二叉树是指一颗二叉树的叶子结点只在最后两层，并且最后一层的叶子结点都集中在左边。显然，满二叉树也是一颗完全二叉树。

遍历二叉树

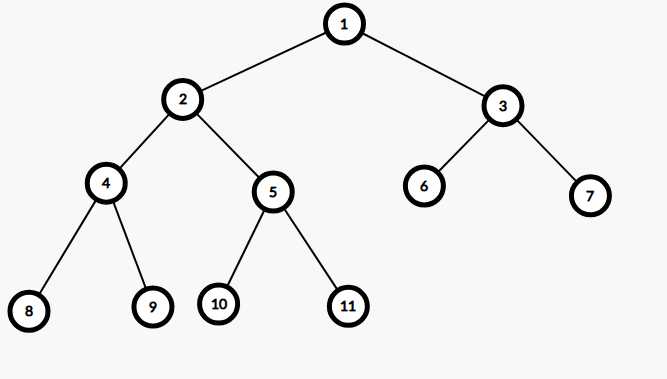
　　对于二叉树的遍历，我们分为三种情况：

一，前序遍历       根结点->左子树->右子树

以下顺序就是124583796

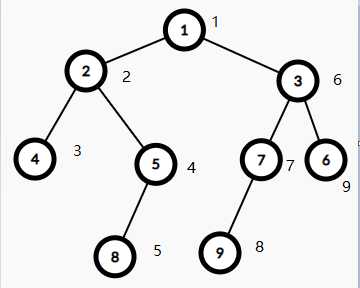
1 void work(int x)
2 {
3     if(!x)return;//如果这个点有效 
4     printf("%d ",x);//根 
5     work(l[x]);//左子树 
6     work(r[x]);//右子树 
7 }

二，中序遍历       左子树->根结点->右子树

以下顺序就是428519736

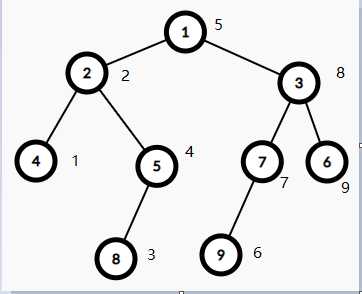
1 void work(int x)
2 {
3     if(!x)return;//如果这个点有效 
4     work(l[x]);//左子树 
5     printf("%d ",x);//根 
6     work(r[x]);//右子树 
7 }

三，后序遍历      右子树 ->左子树->根结点

以下顺序就是485297631

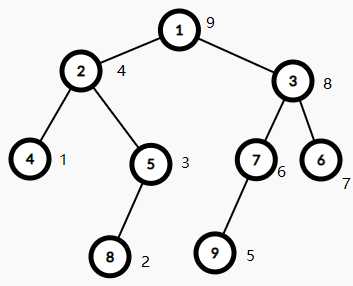
void work(int x)
{
    if(!x)return;//如果这个点有效 
    work(r[x]);//右子树 
    work(l[x]);//左子树 
    printf("%d ",x);//根 
}        

 然而它们之间有神奇的关系

中、后序求先序

P1030 求先序排列

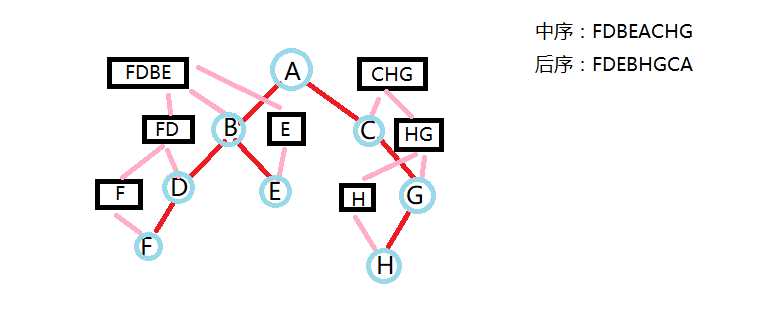
图中粉色的表示这一个序分成了根，左，右三部分（也可能没有左或右）

首先，你要知道，后序的最后一个肯定是根结点，然后你要知道，在一串中序中，找到了它的根结点，那么它左边就是左子树，右边就是右子树。

我们先找到根结点A，然后把中序分为FDBE和CHG左右子树，而左子树的后序就是FDEB，右子树的后序就是HGC，然后一步一步分解下去，知道不能分解，因为我们求先序，所以先输出根结点，然后分别递归左、右子树。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 void beford(string s2,string s3)//中序and后序 
 4 {
 5     if(s2.size()==0)return;
 6     char root=s3[s3.size()-1];//找到根结点 
 7     cout<<root; //输出根结点 
 8     int k=s2.find(root);
 9     beford(s2.substr(0,k),s3.substr(0,k));//左子树 
10     beford(s2.substr(k+1),s3.substr(k,s2.size()-k-1));//右子树 
11 }
12 int main()
13 {
14     string s2,s3;//1，2，3分别对应前，中，后 
15     cin>>s2>>s3; 
16     beford(s2,s3);
17  } 

中、先序求后序

与上面同理，只需要稍微改动一点即可

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 void beford(string s1,string s2)//先序and中序 
 4 {
 5     if(s1.size()==0)return;
 6     char root=s1[0];//找到根结点 
 7     int k=s2.find(root);
 8     beford(s1.substr(1,k),s2.substr(0,k));//左子树 
 9     beford(s1.substr(k+1),s2.substr(k+1));//右子树 
10     cout<<root; //输出根结点 
11 }
12 int main()
13 {
14     string s1,s2;//1，2，3分别对应前，中，后 
15     cin>>s1>>s2; 
16     beford(s1,s2);
17 } 

【常用数据结构——二叉树（还有三叉四叉...？ ）】

标签：一个   ble   遍历   return   ace   problem   get   size   查找树   

原文地址：https://www.cnblogs.com/hualian/p/11344907.html