标签:分支 return load 安全 方案 赛车 input 包含 stream
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 m 条赛道。
C 城一共有 n 个路口,这些路口编号为 1,2,…,n,有 n−1条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 i 条道路连接的两个路口编号为ai? 和 bi?,该道路的长度为li?。借助这n−1 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路e1?,e2?,…,ek?,满足可以从某个路口出发,依次经过 道路e1?,e2?,…,ek?(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 m 条赛道中长度最小的赛道长度最大(即 m 条赛道中最短赛道的长度尽可能大)
输入文件第一行包含两个由空格分隔的正整数n,m,分别表示路口数及需要修建的 赛道数。
接下来 n−1 行,第 i 行包含三个正整数ai?,bi?,li?,表示第 i 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 n−1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
7 1 1 2 10 1 3 5 2 4 9 2 5 8 3 6 6 3 7 7
31
9 3 1 2 6 2 3 3 3 4 5 4 5 10 6 2 4 7 2 9 8 4 7 9 4 4
15
【输入输出样例 1 说明】
所有路口及适合于修建赛道的道路如下图所示:
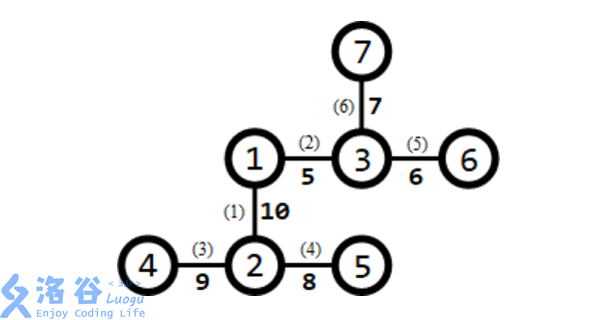
道路旁括号内的数字表示道路的编号,非括号内的数字表示道路长度。 需要修建 1 条赛道。可以修建经过第 3,1,2,6 条道路的赛道(从路口 4 到路口 7), 则该赛道的长度为 9+10+5+7=31,为所有方案中的最大值。
【输入输出样例 2 说明】
所有路口及适合于修建赛道的道路如下图所示:
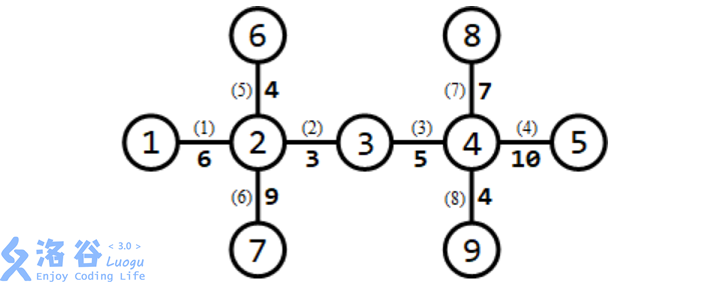
需要修建 3条赛道。可以修建如下 3条赛道:
【数据规模与约定】
所有测试数据的范围和特点如下表所示 :
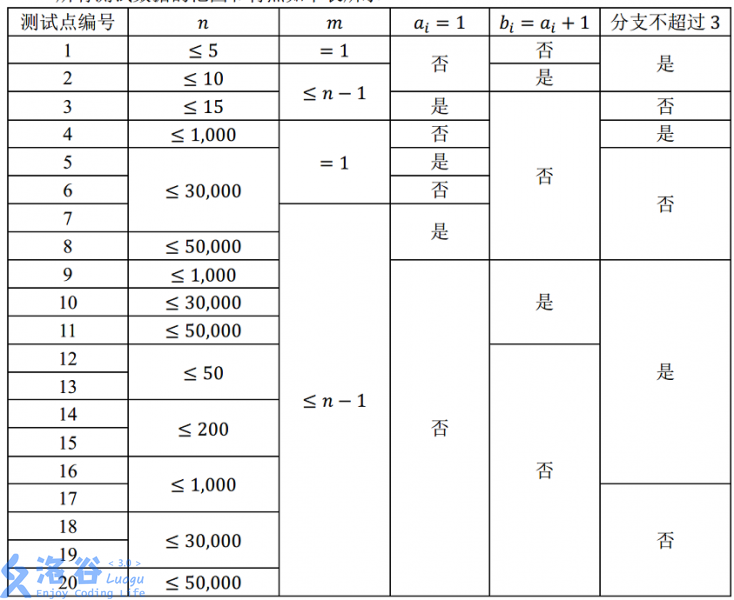
其中,“分支不超过 3”的含义为:每个路口至多有 3 条道路与其相连。 对于所有的数据,2≤n≤50,000, 1≤m≤n−1, 1≤ai?,bi?≤n, 1≤li?≤10,000。
代码:
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=50010;
int n,m,tail;
int head[N],ans[N];
int len[N],arr[N],vis[N];
struct edge {
int v,w,next;
} map[N*2];
void add(int u,int v,int w) {
map[++tail].v=v;
map[tail].w=w;
map[tail].next=head[u];
head[u]=tail;
}
int calc(int tl, int lim) {
int p2=1;
int ans=0;
for(int i=tl; i>p2; i--) {
if(vis[i])
continue;
while(p2<i&&(arr[p2]+arr[i]<lim||vis[p2]))
p2++;
if(p2<i&&!vis[p2]&&arr[i]+arr[p2]>=lim)
ans+=1;
p2++;
}
return ans;
}
void dfs(int u,int f,int lim) {
ans[u]=0;
for(int i=head[u]; i; i=map[i].next) {
if(map[i].v==f)
continue;
len[map[i].v]=map[i].w;
dfs(map[i].v,u,lim);
ans[u]+=ans[map[i].v];
}
int tl=0;
for(int i=head[u]; i; i=map[i].next) {
if(map[i].v==f)
continue;
arr[++tl]=len[map[i].v];
}
if(tl>0) {
sort(arr+1,arr+tl+1);
arr[0]=0;
int vl=calc(tl,lim);
ans[u]+=vl;
int lb=0, rb=tl, res;
while(lb<=rb) {
int mid=(lb+rb)>>1;
vis[mid]=1;
if(calc(tl,lim)==vl) {
res=mid;
lb=mid+1;
} else
rb=mid-1;
vis[mid]=0;
}
len[u]+=arr[res];
}
if(len[u]>=lim) {
len[u]=0;
ans[u]++;
}
}
bool check(int v) {
memset(ans,0,sizeof(ans));
memset(len,0,sizeof(len));
dfs(1,0,v);
return ans[1]>=m;
}
int main () {
memset(vis,0,sizeof(vis));
int l=1,r=0;
int u,v,w,ans;
scanf("%d%d",&n,&m);
for(int i=1; i<n; i++) {
scanf("%d%d%d",&u,&v,&w);
r+=w;
add(u,v,w);
add(v,u,w);
}
while (l<=r) {
int mid=(l+r)>>1;
if(check(mid)) {
ans=mid;
l=mid+1;
} else
r=mid-1;
}
printf("%d",ans);
return 0;
}
标签:分支 return load 安全 方案 赛车 input 包含 stream
原文地址:https://www.cnblogs.com/mysh/p/11351152.html