标签:斐波那契 code wap 一个队列 距离 shu div 方法 出队
左偏树是一种比较常用的可并堆。那什么是可并堆呢?可并堆,顾名思义,是一种除了支持堆的基本操作外,还支持合并等操作的数据结构,如斜堆,左偏树,二项堆,配对堆,斐波那契堆等。
左偏树写起来不难,跑起来也不错 是一个老少咸宜的数据结构
讲解之前先放一张左偏树的概念图:
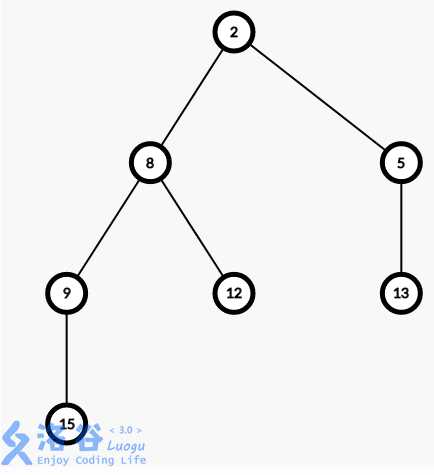
外节点:只有一个儿子或没有儿子的节点,即左右儿子至少有一个为空节点的节点
距离:一个节点到离它最近的外节点的距离,即两节点之间路径的权值和。特别地,外节点的距离为$0$,空节点的距离为$-1$
左偏树:一种满足左偏性质的堆有序二叉树(左偏树的左偏性质体现在左儿子的距离大于右儿子的距离)
左偏树的距离:我们将一棵左偏树根节点的距离作为该树的距离
满足堆的基本性质
对于任意节点,左儿子的距离大于右儿子的距离
对于任意节点,其距离等于它的右儿子的距离加一
对于一棵$n$个节点的左偏树,其根节点的距离不超过$log^N$
对于一棵距离为$d$的左偏树,其节点数不少于$2^{k+1}-1$
左偏树一般存储以下几个节点信息,这里先写出来,方便之后的讲述。(具体实现时还是要根据题目需求来存储信息,这里给出几个基本的)
合并
合并是左偏树最重要的操作,毕竟可并堆可并堆,肯定是要能够合并的。
定义一个函数$Merge(x,y)$表示合并$x,y$,返回值为合并后的根节点。具体实现流程如下:
(若$x$的权值大于$y$,交换$x,y$即可)。递归地向下合并,在$x$的右子树最右链中找到第一个权值大于$y$的权值的节点$k$,将$y$作为$k$的父亲。
2.继续递归,合并$y$的右子树和$k$的右子树,直到$x$或$y$为空。
3.在合并的过程中注意维护左偏性质,即若左儿子的距离小于右儿子的距离,则交换左右儿子。
合并代码:
int Merge(int x,int y)
{
if(!x || !y)
return x+y;
if(v(x)>v(y) ||(v(x)==v(y) && x>y))
swap(x,y);
int &ls=l(x),&rs=r(x);
rs=Merge(rs,y);
f(rs)=x;
if(d(ls)<d(rs))
swap(ls,rs);
d(x)=d(rs)+1;
return x;
}
删除根节点
只要先删除根节点,即将根节点的权值赋为$-1$(其实有的时候不改权值也没影响),然后合并根节点的左右子树就可以了。
删除根节点代码:
void Delroot(int x)
{
int ls=l(x),rs=r(x);
v(x)=-1,f(ls)=0,f(rs)=0;
Merge(ls,rs);
}
删除任意节点
这里的任意节点指的是任意编号的节点而不是任意权值的节点,一般的可并堆是不支持删除给定权值节点的操作的。
与删除根节点类似,先将要删除的节点的权值赋值为$-1$,然后合并它的左右子树,将合并后新的左偏树接到被删除节点的父节点上就可以了。但是与删除根节点不同的是,这个操作可能会导致整棵左偏树的左偏性质被破坏,因此要从该节点一直向上检查左偏性质,直到左偏性质没有被破坏或者到达了根节点。
删除节点代码:
void Delete(int x)
{
int fx=f(x),p=Merge(l(x),r(x));
int &ls=l(fx),&rs=r(fx);
f(p)=fx;
ls==x?ls=p:rs=p;
while(p)
{
if(d(ls)<d(rs))
swap(ls,rs);
if(d(fx)==d(rs)+1)
return ;
d(fx)=d(rs)+1;
p=fx,fx=f(x);
ls=l(fx),rs=r(fx);
}
}
建树
暴力加点合并的话时间复杂度是$O(nlogn)$,令人难以接受,因此我们需要一个比较高效的方法来实现建树。
建树有以下几个步骤:
1. 建立一个队列,将每个节点看作一个节点数为$1$的左偏树加入队列。
2. 每次取出队头的两棵左偏树,将它们合并,并将合并后的新左偏树加入队列。
3. 重复第$2$步,直到队列为空。
建树代码:
void Build()
{
queue<int> q;
for(int i=1;i<=n;i++)
q.push(i);
int x,y;
while(q.size())
{
x=q.front();q.pop();
y=q.front();q.pop();
q.push(Merge(x,y));
}
}
习题:
参考资料:
2019.7.11 于厦门外国语学校石狮分校
标签:斐波那契 code wap 一个队列 距离 shu div 方法 出队
原文地址:https://www.cnblogs.com/TEoS/p/11351372.html