标签:cti app lin dap ocp 函数 div als cal
我们有三种曲线:
A curve that we know is "above" the running time function when n is large. ( Big-O )
当n足够大时,曲线高于运行时间函数(big-o)
A curve that we know is "below" the running time function when n is large. (Big-Omega)
当n足够大时,曲线低于运行时间函数(big-omega)
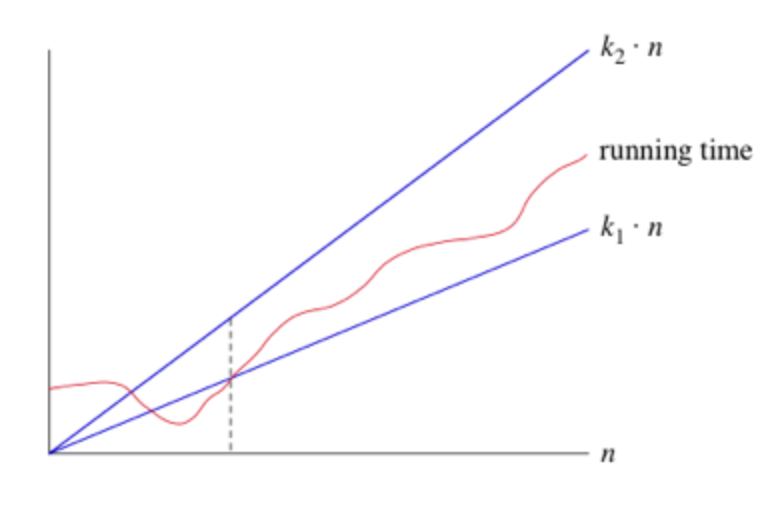
If we can squeeze the curves that are "above" and "below" the running time function close enough, then we can figure out Big-Theta(big-theta)
Big-Theta 仅仅只是一个"Scaled"版本的运行曲线,big-theta仅仅只是scale最高序列的f(n)行为。big-theta仅仅只是一个曲线
Big-O 告诉你什么样的函数增长速度大于f(N)
Bit-Theta告诉你什么样的函数增长速度同f(N)
Big-Omega告诉你什么样的函数增长速度小于f(N)
Funcitons in Asymptotic notation
?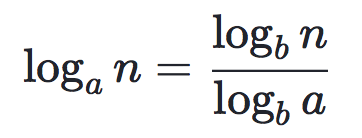 ?
?
所有公式都可以用这个来表示
Logarithms grow more slowly than polynomials
对数比指数增长慢
接下来是指数增长的顺序(由慢到快):
?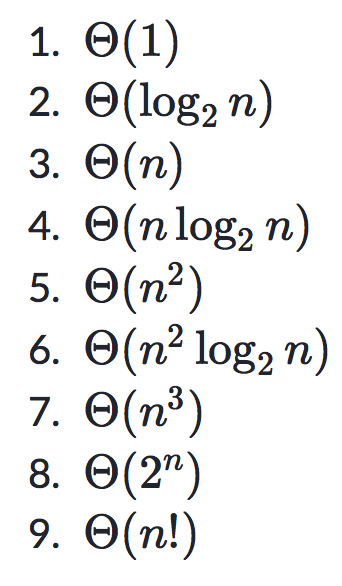 ?
?
? ?
?
? ?
?
It would be convenient to have a form of asymptotic notation that means
运行时间最多增长这么多,但它可以增长的更慢
big-O asymptotic upper bounds:渐近上界
best case average/expected case worst case
时间复杂度big-O、Big-Omega和big-Theta
标签:cti app lin dap ocp 函数 div als cal
原文地址:https://www.cnblogs.com/zhichun/p/11361222.html