标签:dfs dde include 个人 print nio inf 两种 pop
题意:给你n个点 每个点都有两种选择 成为战士或者法师 现在给你m个关系 对应这两个人的对应关系的权值A,B,C
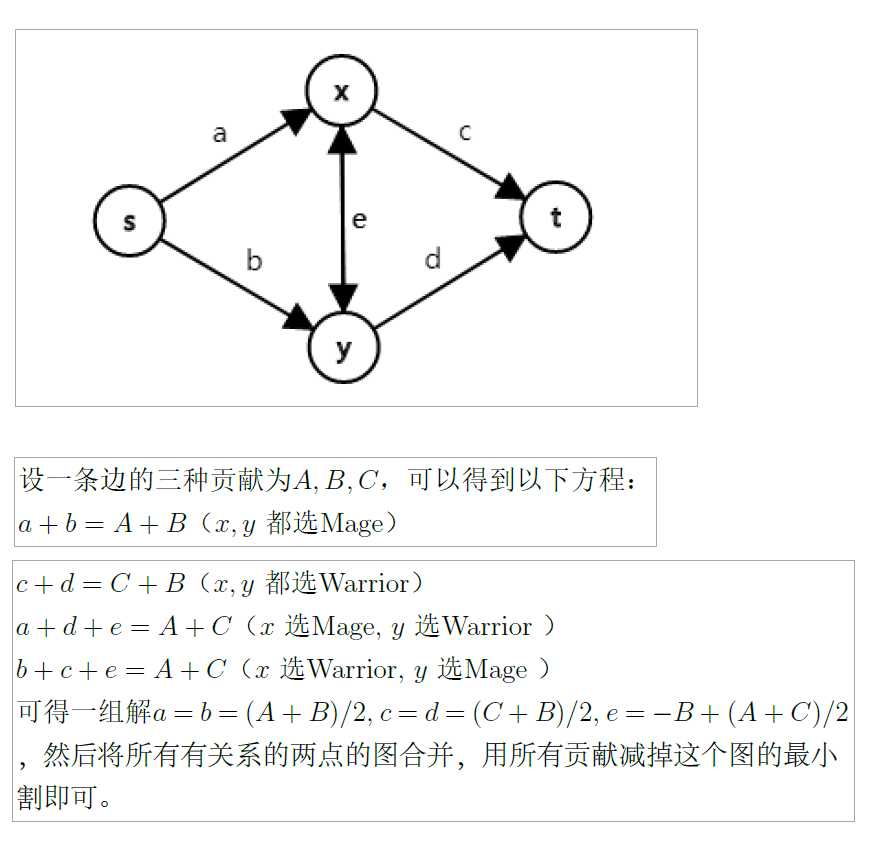
思路:按照下面的思路建图跑最小割(要注意权值要乘2 可能存在不整除的情况)
#include <bits/stdc++.h> using namespace std; const double pi = acos(-1.0); const int maxn = 1e3+7; const int inf = 0x3f3f3f3f; const double eps = 1e-6; typedef long long ll; const ll mod = 1e7+9; struct Edge { ll from, to, cap, flow; Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {} }; struct Dinic { int n, m, s, t; vector<Edge> edges; vector<int> G[maxn]; int d[maxn], cur[maxn]; bool vis[maxn]; void init(int n) { for (int i = 0; i < n; i++) G[i].clear(); edges.clear(); } void AddEdge(int from, int to, int cap) { edges.push_back(Edge(from, to, cap, 0)); edges.push_back(Edge(to, from, 0, 0)); m = edges.size(); G[from].push_back(m - 2); G[to].push_back(m - 1); } bool BFS() { memset(vis, 0, sizeof(vis)); queue<int> Q; Q.push(s); d[s] = 0; vis[s] = 1; while (!Q.empty()) { int x = Q.front(); Q.pop(); for (int i = 0; i < G[x].size(); i++) { Edge& e = edges[G[x][i]]; if (!vis[e.to] && e.cap > e.flow) { vis[e.to] = 1; d[e.to] = d[x] + 1; Q.push(e.to); } } } return vis[t]; } ll DFS(int x, ll a) { if (x == t || a == 0) return a; ll flow = 0, f; for (int& i = cur[x]; i < G[x].size(); i++) { Edge& e = edges[G[x][i]]; if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) { e.flow += f; edges[G[x][i] ^ 1].flow -= f; flow += f; a -= f; if (a == 0) break; } } return flow; } ll Maxflow(int s, int t) { this->s = s; this->t = t; ll flow = 0; while (BFS()) { memset(cur, 0, sizeof(cur)); flow += DFS(s, inf); } return flow; } }dinic; int main(){ int n,m; while(~scanf("%d%d",&n,&m)){ dinic.init(n+2); ll sum=0; for(int i=1;i<=m;i++){ int u,v; ll A,B,C; scanf("%d%d%lld%lld%lld",&u,&v,&A,&B,&C); sum+=2*(A+B+C); ll a,b,c,d,e; a=b=(A+B); c=d=(B+C); e=-2*B+(A+C); dinic.AddEdge(0,u,a); dinic.AddEdge(0,v,b); dinic.AddEdge(u,v,e); dinic.AddEdge(v,u,e); dinic.AddEdge(u,n+1,c); dinic.AddEdge(v,n+1,d); } printf("%lld\n",(sum-dinic.Maxflow(0,n+1))/2); } }
2019 Multi-University Training Contest 2 Harmonious Army(最小割)
标签:dfs dde include 个人 print nio inf 两种 pop
原文地址:https://www.cnblogs.com/wmj6/p/11366536.html