标签:其他 矩阵 有一个 读者 master log strong 固定 reg
做完之后看了看题解,怎么一篇和我思路一样的也没有...我好慌啊qwq(所以一定是窝太弱了看不懂dalao的思路)
好吧窝的方法确实很奇怪:
核心代码只有3行 输入 循环 输出 一气呵成 是题解中的豪杰
最重要的是
(只有我们的好朋友gcd
咳咳 那么开始正题(敲黑板)
首先,我们定义一个网格被一个三角形完全覆盖,当且仅当这个三角形的三个顶点都在网格边界上,并且沿着网格内部任意一条线段把网格切开,一定会把三角形切成两部分。比如下面的例子就是一个完全覆盖(渣鼠绘):
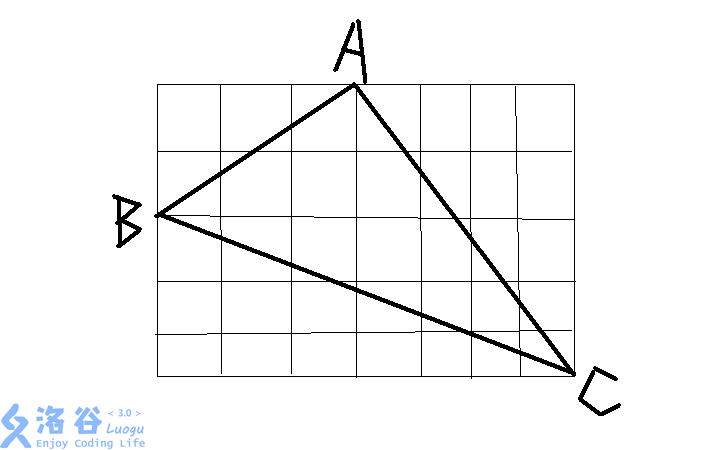
但是这个就不是:(因为沿红色竖线切开,并不能切到三角形)
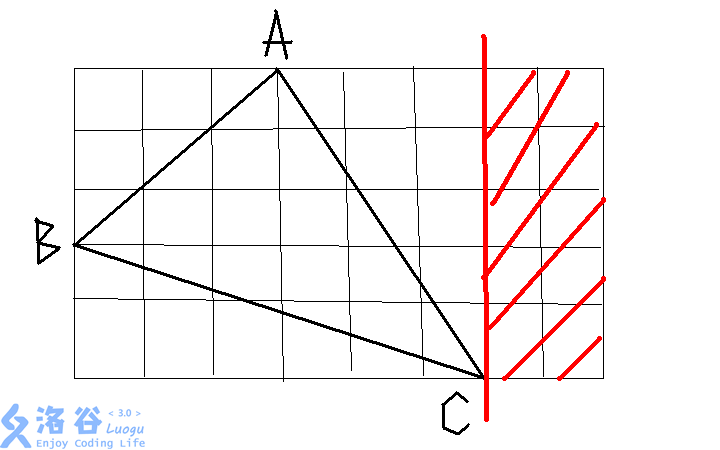
那么我们发现:
——但是子矩形好多啊,枚举左上角和右下角,至少是\(n^2m^2\)的数量级哇qwq
——[恋符]MasterSpark.gif 注意到我们并不关心每个子矩形的位置,而只关心它们的长宽,以及长宽均相同的矩形的数目,所以枚举子矩形的长 \(i\) 和宽 \(j\),则\(i*j\)的矩形数量为\((n-i+1)*(m-j+1)\),子矩阵数量级降为\(nm\)。
至此,原问题转化为
**给定网格的长宽,迅速求解完全覆盖网格的三角形的数目**继续观察,我们发现:
首先分析只有一个顶点在\(MNPQ\)角上的情况。不妨设\(A\)点与\(M\)点重合,为了使\(ABC\)完全覆盖\(MNPQ\),\(B\)和\(C\)必须分别在\(NP\)和\(PQ\)边上(如下图):

显然对于一个\(i*j\)的网格(这里\(i\) \(j\)指的是空格的数量而非格点,上图\(i=6,j=10\)),固定顶点的位置有四种,每种对应的另外两个顶点的位置有\((i-1)*(j-1)\)种(\(B\) \(C\)不能与\(N\) \(P\) \(Q\)重合),共\(4*(i-1)*(j-1)\)种。
分析两个顶点在\(MNPQ\)角上的情况。不妨设\(A\)与\(M\)重合。此时另外一个角上的点(不妨设为点\(B\))有三种情况:
1、\(B\)与\(N\)重合。此时\(C\)一定在\(QP\)上。共\((i-1)\)种情况。
2、\(B\)与\(Q\)重合。此时\(C\)一定在\(NP\)上。共\((j-1)\)种情况。
3、\(B\)与\(P\)重合。
这是比较麻烦的一种状态,因为此时\(C\)点可以在网格中能构成三角形的任意一处。但是我们注意到,如果线段\(AB\)除了经过\(M\) \(P\)之外,还经过了一些其他格点,\(C\)是不能与它们重合的。
那么有多少个格点被\(AB\)穿过呢qwq?
显然,不包括\(AB\)本身,有\(gcd(i,j)-1\)个(至于为什么,请读者自己思考(明明就是你自己也不会证吧kora
所以第三种情况的方案数是\((i+1)*(j+1)-4-gcd(i,j)+1\)(这里\(-4\)是因为C点不能放在网格的四个角上)。
注意到以上三种情况都可以反转,从而得到另一组与其一一对应的方案。
分析三个顶点在\(MNPQ\)角上的情况。显然只有四种。
综上,对于一个长宽为\(i,j\)的网格,可以把它完全覆盖的三角形的个数
\(S=4*(i-1)*(j-1)+2*[(i-1)+(j-1)+(i+1)*(j+1)-4-gcd(i,j)+1]+4\)
\(=6*i*j-2*gcd(i,j)\)
枚举子矩阵的复杂度为\(mn\),单次求解\(gcd\)的复杂度为\(log(m+n)\),总复杂度\(O(mnlog(m+n))\),实际运行跑的飞起。
下面是AC代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
#define ll long long
using namespace std;
int getgcd(int a, int b)
{
if (!b) return a;
return getgcd(b, a % b);
}
int main()
{
ll n, m, ans = 0;
cin >> n >> m;
for (R int i = 1; i <= n; ++i)
for (R int j = 1; j <= m; ++j)
ans += (n - i + 1) * (m - j + 1) * (6 * i * j - 2 * getgcd(i, j));
cout << ans;
return 0;
}那么这篇文章就到这里,希望对您能有帮助。ありがとナスます~
标签:其他 矩阵 有一个 读者 master log strong 固定 reg
原文地址:https://www.cnblogs.com/suwakow/p/11375053.html