纪中第十八天

标签：答案   精度   mamicode   ali   状态   判断   任务   pac   动态规划   

第二题 简单游戏(DFS)

分析：题目要求1-N的一个排列A₁,A₂…A_n使得C(N-1,0)*A₁+C(N-1,1)*A₂+….+C(N-1,N-1)*A_N=T,

即：     -----①式

方法很好确定，先把C（N-1，i）求出来，然后只要把每一个位上的数确定好就可以了，所以采用深度优先搜索的方法。

方法：直接搜，用DFS(x,y)表示当前将要确定第x个位置上数，已经确定的和为y，把每种情况都搜出来，然后在递归出口的位置判断①式是否成立，不过很可惜，这种方法得不到分；

剪枝一：加一个小小的优化，就是在确定第X个数时，保证新求出来的y不能大于T，加上这个优化后，可以得40分；

剪枝二：由于C(N-1,i)=C(N-1,N-1-i)，具有对称性，题目又要求最小字典序列，所以在枚举时当x>n div 2 时，要保证a[x]>a[N+1-x],这样程序速度会提高，但是该题还是只能得40分；

剪枝三：当枚举到第X个数时，剩余的N-X个数，与剩余的N-X个系数一一对应，让大数和大系数相乘，小数和小系数相乘可以得到最大值，让大数和小系数相乘，小数和大系数相乘可以得到最小值，如果剩余的值不在这个范围内，就不要搜下去，这样可以大大优化，拿样例举例来说：

N=4，T=16

当枚举a[1]=1时，剩余16-1*1=15，剩余的未放置的数为2，3，4，剩余的系数为1，3，3，这样最大值为4*3+3*3+2*1=23，最小值为4*1+3*3+2*3=19，都超过了15，所以第一个数不能选1。

第三题 幸运票(递推)

分析：题目要求组成一个2*N的数，前N位的和等于后N位的和=S/2，首先考虑两个特殊情况：(1)N为奇数，答案为0(2)S=0和S=18*N，答案为1。

另前N的数字和为S/2的方法数=后N位数字和为S/2的方法数，所以答案等于ANS^2,ANS表示N的数字和为S/2的方法数，现在的任务就是计算ANS，很容易想到用状态f[i,j]表示i个数和为j的方法，那么ANS=f[N,S/2],怎么计算f[i,j]呢？可以从“第i上的数字是多少？”这个问题得到递推方程式：

          (1)j>9*i时：f[i,j]=0  

f[i,j]=   (2)(i=1)AND(0<=j<=9):f[1,j]=1

          (3)i>1时：f[i,j]=

时间复杂度为O(N*S*10),另f[i,j]具有对称性：f[i,j]=f[i,9*i-j],可以把效率提高一倍。另有5个数据答案很大，要用高精度。

第四题 抄书(动态规划或二分法)

方法一：动态规划

定义f[i,j]表示把前i本书分给j个人来抄的最小值，那么f[N,M]就是答案，定义s(i,j)表示第i本书到第j本书的页数和，通过分析“第j个人抄哪些书？”这个问题，得到以下状态转移方程：

         (1)j=1时：f[i,1]=s(1,i)

f[i,j]=

(2)j>1时：max(f[k,j-1],s(k+1,i))，其中j-1<=k<i

该算法的时间复杂度为O(N*M*M)，对于较大数据会超时，要继续优化：

优化如下：

f[i,j]的值随着k的变化有可能形成一个抛物线，我们可以在出现拐点的地方停止对K的枚举，提高程序的效率，大家可以参考下图：

                F[i,j]

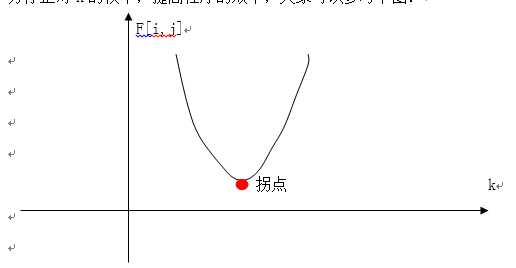
拐点                         k

上面的优化大家可以参考标程里book(CQF).pas程序。

方法二：二分答案法

L为左边界，R为右边界，

(1)如果L<=R,做第二步

(2)M=(L+R)DIV 2

(3)构造答案为M的方案，从后往前遵循能尽可能多抄的原则，求出所需人数X

(4)如果X<=M,执行R=M-1,否则L=M+1,转入第(1)步

最后的答案为L，该方法的时间复杂度为O(N*lg(P)),其中P=,可以参考标程里book.pas。

以下是样例的二分过程：

vvf

纪中第十八天

标签：答案   精度   mamicode   ali   状态   判断   任务   pac   动态规划   

原文地址：https://www.cnblogs.com/WestJackson/p/11383773.html