标签:src lse 路径 span 初始化 line main add 也会
一种最短路求法(个人觉得比DIJKSTRA好用)
用于有向图。
大概思路:从根节点开始,枚举每一个点,同时更新他们所联通的点的最短路径,如果路径被更新,则把这个点入队,一直重复这个操作直到队伍为空为止。
代码:
struct edge { int next, to, v; }e[];//存图,next代表同一个头结点的下一条边 void spfa(int S) { int p, x, y, l, r; for (x = 1; x <= n; ++x) dis[x] = inf; q[0] = S, dis[S] = 0, v[S] = 1;//初始化 for (l = r = 0; l != (r + 1) % N; ) { p = q[l], ++l %= N;//每次取出队首 for (x = first[p]; x; x = e[x].next)//遍历与队首同头的每一条边 if (dis[p] + e[x].v < dis[(y = e[x].to)]) {//如果可以更新 dis[y] = dis[p] + e[x].v;//更新 if (!v[y]) { v[y] = 1; q[++r %= N] = y;//入队 } } v[p] = 0; } }
但是这种做法容易被卡掉(神奇奶牛),所以可以采用SLF优化。
SLF优化:每一次都把即将入队的值与队首值比较,若比队首值小,则存入队首。
为什么呢?
因为每一次都会从队首开始遍历,当队首是最小值时,被更新的所以节点的值也会是最小值,这样可以节省很大一部分时间。
(有点抽象。。举个例子吧)
(我不想画图)
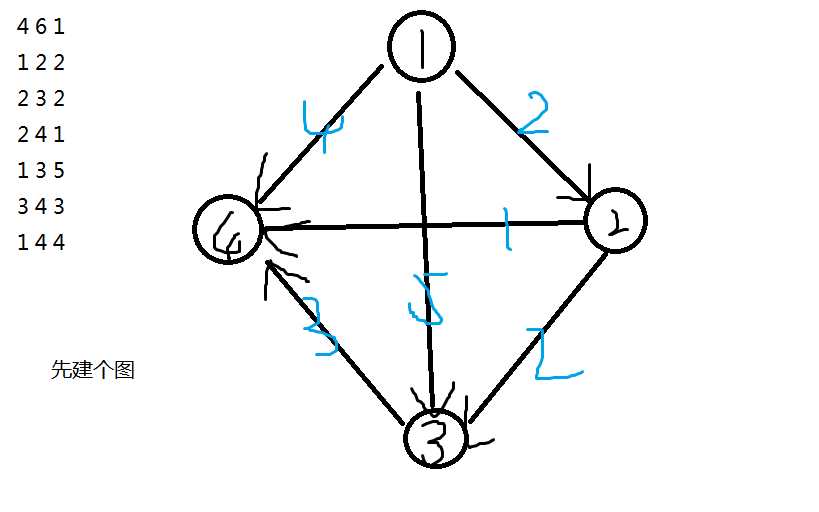
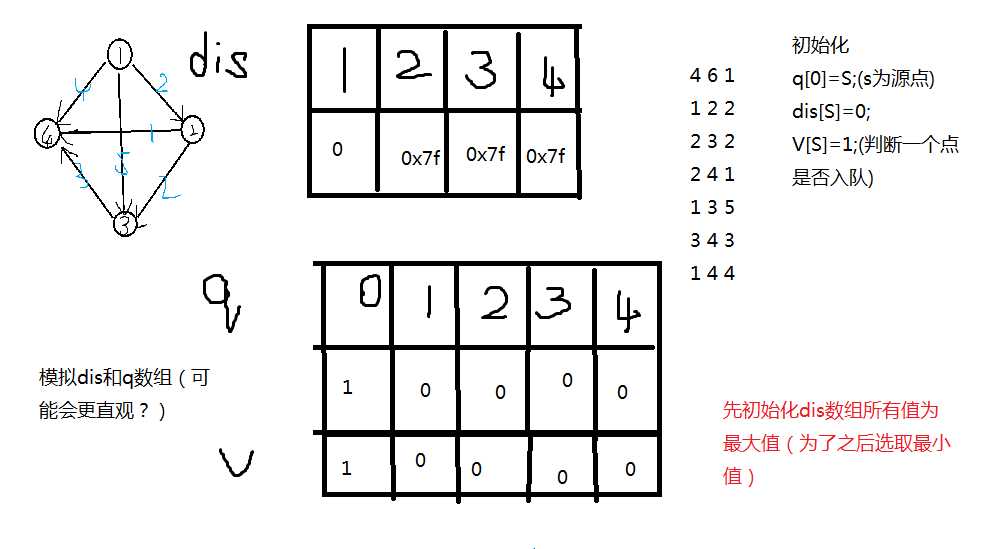
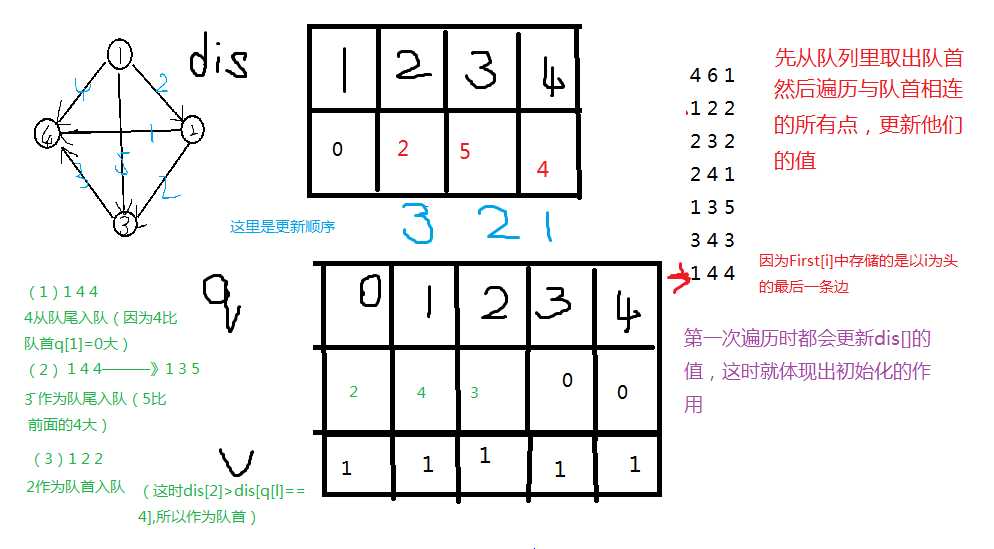
这里需要注意:只有dis[]存储路径值,q[]存储的是当前最小路径值所在的位置,包括edge里的next也是同一个起点的上一对点的序号。(这里的头就是First[]的下标)
这里各种各样的序号很多。。特别容易弄混。会把各种序号分段输出的程序放在结尾,看不懂的话试几组样例看看输出会很有帮助。
到这里只是第一次更新。
下面是第二次更新:
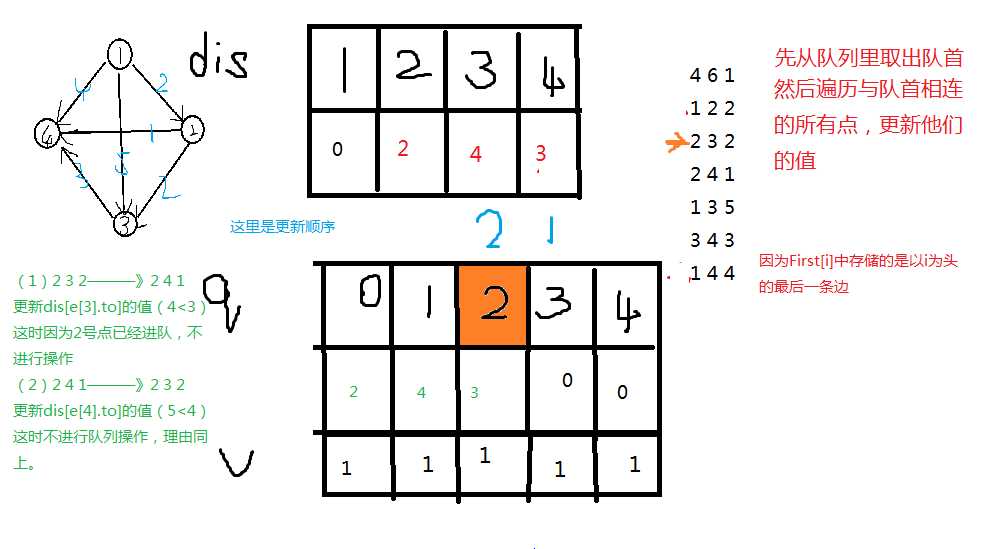
接下来就可以以此类推了。。如果看不懂的话下面是分段输出的代码,结合上面的图看,体会一下中心思想。
代码:
#include<iostream> using namespace std; struct edge { int next, to, v; edge(){} edge(int x,int y,int z) { next=x; to=y; v=z; } }e[10001]; int first[10001]; int tot; int dis[100001]; int q[100001]; int v[100001]; void add_edge(int x, int y,int z) { e[++tot] = edge(first[x], y,z); first[x] = tot; } int n; int N=31; int inc(int x) { x = x + 1; x = x % N; return x; } int dec(int x) { x = x - 1 + N; x = x % N; return x; } void spfa(int S) { int p, x, y, l, r; for (x = 1; x <= n; ++x) dis[x] = 0x7ffff; q[0] = S, dis[S] = 0, v[S] = 1; for (l = r = 0; l != (r + 1) % N; ) { p = q[l]; cout<<"从第"<<p<<"号边开始遍历"<<endl; l=inc(l); for (x = first[p]; x; x = e[x].next) { cout<<"这时是第"<<x<<"号边"<<endl; if (dis[p] + e[x].v < dis[(y = e[x].to)]) { cout<<"更新"<<" "<<"将"<<dis[y]; dis[y] = dis[p] + e[x].v; cout<<"更新为"<<dis[y]<<endl; if (!v[y]) { v[y] = 1; if (dis[y] < dis[q[l]]) {q[(l=dec(l))] = y; cout<<"从队首插入"<<y<<endl; cout<<"这时l为"<<l<<"r不变"<<endl; } else {q[(r=inc(r))] = y; cout<<"从队尾插入"<<y<<endl; cout<<"这时l不变r变为"<<r<<endl; } cout<<"更新后的队列为"<<endl; for(int i=0;i<=n;i++) { cout<<q[i]<<" "; } cout<<endl; cout<<"入队情况为"<<endl; for(int i=1;i<=n;i++) cout<<"第"<<i<<"号元素"<<v[i]<<" "; cout<<endl; } } } v[p] = 0; cout<<"此时最短路径被更新为"<<endl; for(int i=0;i<=n;i++) { cout<<dis[i]<<" "; } cout<<endl; } } int main() { int m,S; cin>>n>>m>>S; int x,y,z; for(int i=1;i<=m;i++) { cin>>x>>y>>z; add_edge(x,y,z); } spfa(S); cout<<"最终最短路径"<<endl; for(int i=1;i<=n;i++) { cout<<dis[i]<<" "; } cout<<"一共有"<<tot<<"个节点,分别是"<<endl; for(int i=1;i<=tot;i++) { cout<<"与它同起点的上一对点为"<<e[i].next<<"号"<<" "<<"它指向"<<e[i].to<<"这个点"<<endl; } cout<<"下面输出First数组"<<endl; for(int i=1;i<=tot;i++) { cout<<first[i]<<" "; } }
这是举例用的样例:
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
到这里就结束啦!希望可以看懂!
蒟蒻的第二篇博客(再放个烟花吧!)
标签:src lse 路径 span 初始化 line main add 也会
原文地址:https://www.cnblogs.com/Daz-Os0619/p/11388157.html