标签:空间 ble 现在 tps 分析 java null 使用 byte
跳表也叫跳跃表,是一种动态的数据结构。如果我们需要在有序链表中进行查找某个值,需要遍历整个链表,二分查找对链表不支持,二分查找的底层要求为数组,遍历整个链表的时间复杂度为O(n)。我们可以把链表改造成B树、红黑树、AVL树等数据结构来提升查询效率,但是B树、红黑树、AVL树这些数据结构实现起来非常复杂,里面的细节也比较多。跳表就是为了提升有序链表的查询速度产生的一种动态数据结构,跳表相对B树、红黑树、AVL树这些数据结构实现起来比较简单,但时间复杂度与B树、红黑树、AVL树这些数据结构不相上下,时间复杂度能够达到O(logn)。

要理解跳表,我们先从有序链表开始,对于上图中的有序链表,我们要查找值为150的节点,我们需要遍历到链表的最后一个元素才能找到,用大O表示时间复杂度就为O(n)。时间复杂度比较高,有没有优化空间呢?答案是肯定的,我们采取空间换时间的概念,对链表抽取出索引层,比如每两个元素抽取一个元素构成新的有序链表,这样索引层的有序链表相对底层的链表来说长度更短、间距更大,改造之后的链表入下图所示:
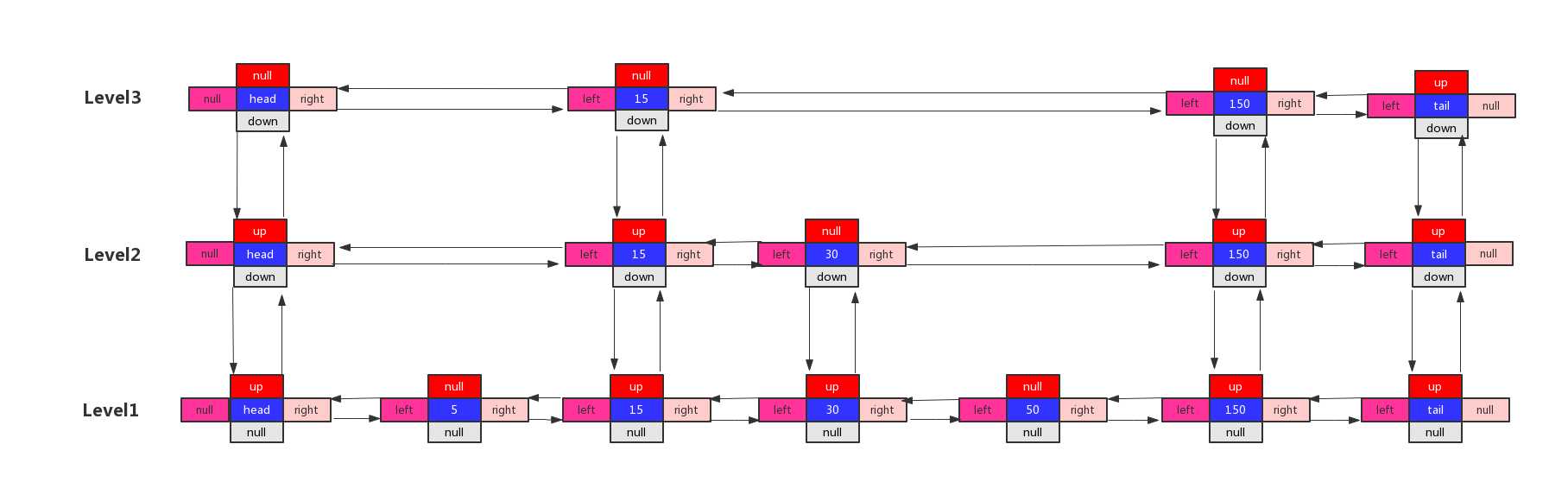
我们在新的链表中查询150,先从最上层Level3开始查找,遍历Level3有序链表,遍历两次就查询到了150这个节点。相对于初始链表来说,改造后的链表对查询效率有了不少的提升。
改造后的链表就是跳表,跳表采用的是以空间换时间的概念,将有序链表随机抽出好几层有序链表,查找的时候先从最上层开始,然后一直下沉到最底层链表。
现在我们对跳表有了一定的认识,总结一下跳表的性质:
跳表一般使用单链表来实现,这样比较节约空间。我使用双向链表来实现跳表,因为双向链表相对单向链表来说比较容易理解跳表的实现。
// 头节点
private final static byte HEAD_NODE = (byte) -1;
// 数据节点
private final static byte DATA_NODE = (byte) 0;
// 尾节点
private final static byte TAIL_NODE = (byte) -1;
private static class Node{
private Integer value;
// 上下左右节点
private Node up,down,left,right;
private byte bit;
public Node(Integer value,byte bit){
this.value = value;
this.bit = bit;
}
public Node(Integer value){
this(value,DATA_NODE);
}
}跳表的搜索从最上层开始查询,最开始的节点p指向最顶层的head节点,如果p.right.value小于等于带查询元素,则p指向p.right,否则指向p.down。直到p.down为空,返回该节点。
跳表查找示意图:
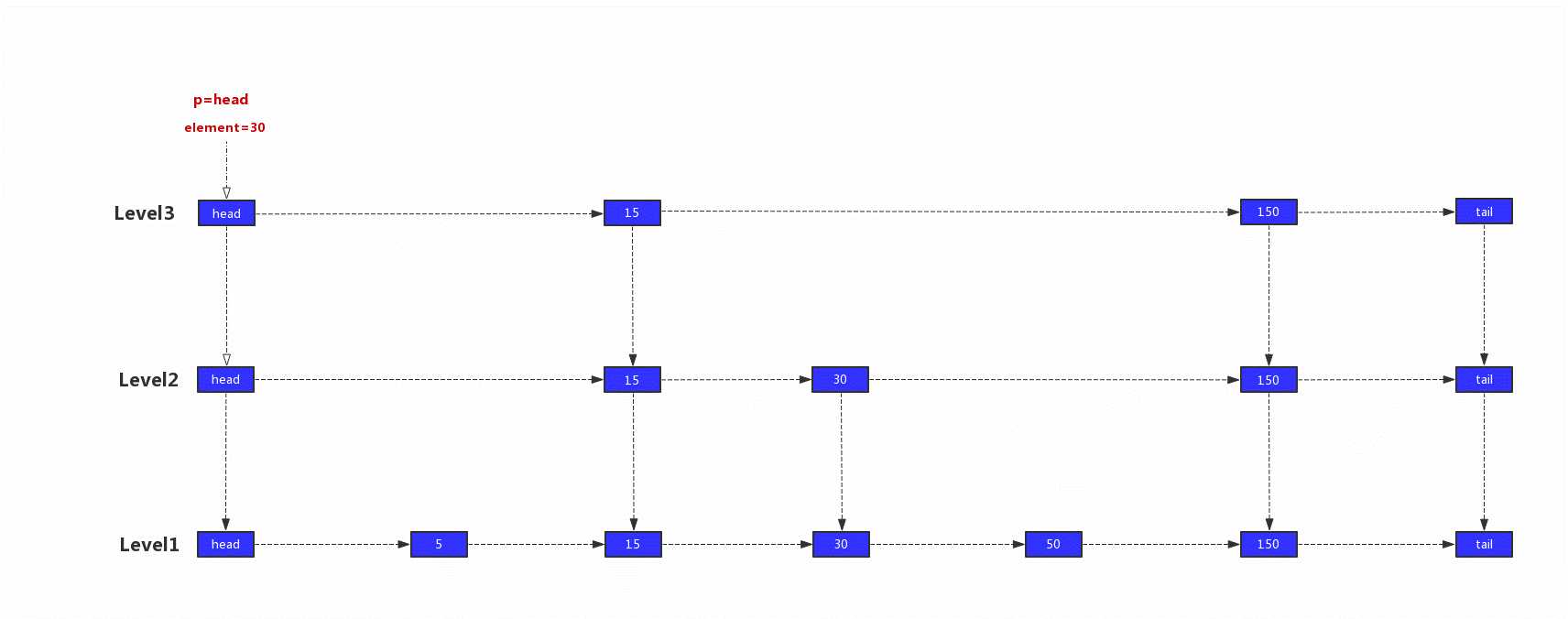
1)p=head,head.right.value=15,15<30,继续往右边查找,p=head.right
2)p.right.value=150,150 > 30,往下一层查找,p=p.down
3)p.right.value=30,30=30,继续往右边查找,p=p.right
4)p.right.value=150,150 > 30,往下一层查找,p=p.down
5)p.right.value=50,50 > 30,由于p.down为空,所以就返回该节点
/**
* 通用查找
* 查找出最后一个小于该元素或者等于元素的节点
* @param element 待查找的数
* @return
*/
private Node find(Integer element){
Node current = head;
for (;;){
while (current.right.bit !=TAIL_NODE && current.right.value <= element){
current = current.right;
}
if (current.down !=null){// 找到最底层节点
current = current.down;
}else{
break;
}
}
return current;// current.value <= element <current.right.value
}
/**
* 获取某个元素
* @param element
* @return
*/
public Integer get(Integer element){
Node node = this.find(element);
return (node.value==element)?node.value:null;
}理解了跳表的查找后,在来看跳表的插入就相对来说比较简单,我们先找出最后一个小于等于插入值的节点,我们将值插入到该节点的右边。除了最底层链表上的插入外,每个新插入的节点都会有一个随机的层高,我们还需要维护层高之间的节点关系,因为新节点的左边第一个元素不一定有层高,所以我们要往左边查找到第一个node.up不为空的节点,维护节点之间的关系,然后将节点作为新的节点,继续往上加层。
我们以值55,层高为2的新节点为例,演示索引建立的过程。
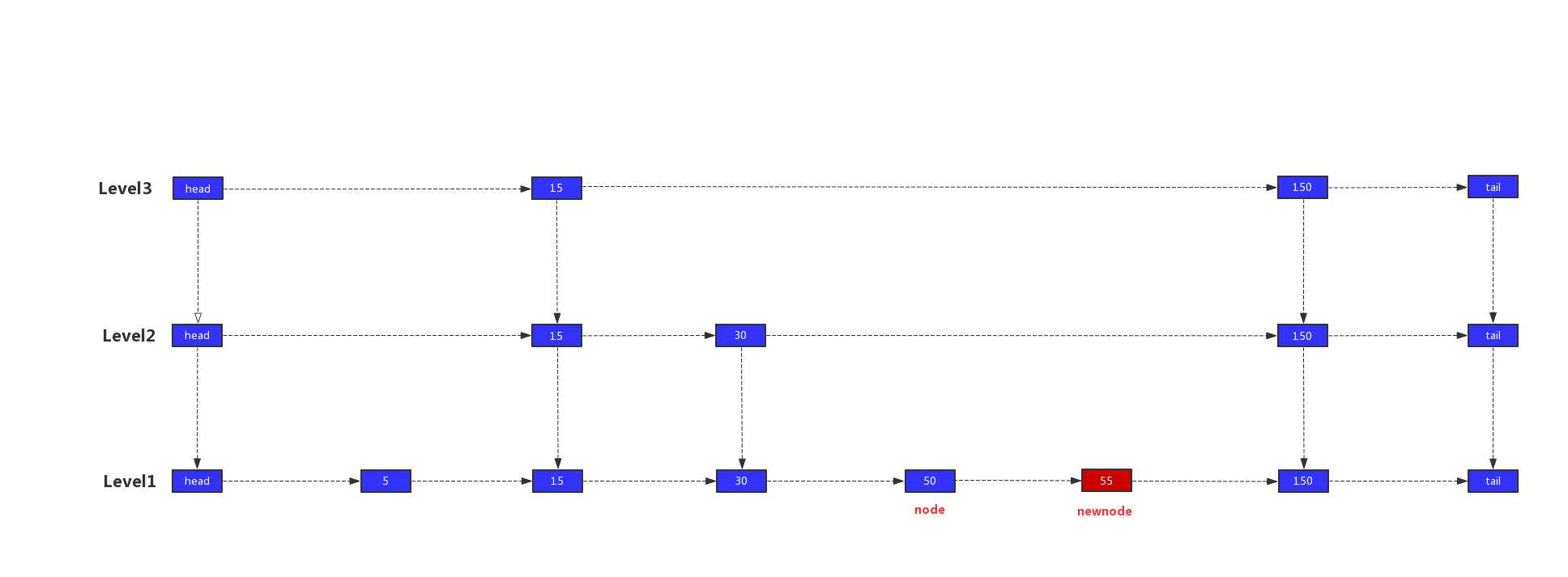
1)我们先找出最后一个小于或者等于插入值的节点,即图中的node节点,然后将新节点插入到node的右边,即newnode节点。
2)node=50时,node.up为空,所以node = node.left
3)node=30时,node.up不为空,此时node=node.up
4)此时node已经移到level2的30节点上,在node的右边建立indexNode节点,作为新插入值的lebel2层的索引
5)将indexNode节点作为新的newnode节点继续向上添加索引,由于我们新插入节点的层高为2,所以将结束循环,新增元素完毕。
/**
* 添加元素
* @param element
*/
public void add(Integer element){
//查找出前一个节点
Node node = this.find(element);
// 新建节点
Node newNode = new Node(element);
// 新节点与前后两节点建立关系
newNode.left = node;
newNode.right = node.right;
node.right.left = newNode;
node.right = newNode;
int currentLevel = 1;
// 建立索引层,随机建立层高
while (random.nextDouble() < 0.5d){
// 索引大于当前索引层
if (currentLevel >= level){
level++;
// 最顶层索引的头指针
Node topHead = new Node(null,HEAD_NODE);
// 最顶层索引的尾指针
Node topTail = new Node(null,TAIL_NODE);
topHead.right = topTail;
topHead.down = head;
head.up = topHead;
topTail.left = topHead;
topTail.down = tail;
tail.up = topTail;
head = topHead;
tail = topTail;
}
// 一直往左边找到索引层
while (node !=null && node.up == null){
node = node.left;
}
node = node.up;
// 新建索引节点,与当前左边节点建立关系
Node indexNode = new Node(element);
indexNode.left = node;
indexNode.right = node.right;
indexNode.down = newNode;
node.right.left = indexNode;
node.right = indexNode;
newNode.up = indexNode;
// 将索引节点作为新的节点,继续往上建立索引(如果有索引的话)
newNode = indexNode;
currentLevel++;
// 当前层高大于最高层高时,跳出循环
if (currentLevel > MAX_LEVEL) break;
}
size ++;
}跳表的删除就比较简单,找到该节点,从最底层开始删除,直到node.up为空。
/**
* 删除跳表
* @param element 待删除的元素
*/
public void delete(Integer element){
Node node = this.find(element);
// 没有找到该元素,直接返回
if (node.value != element) return;
// 删除元素,将元素的左右链表建立关系
node.left.right = node.right;
node.right.left = node.left;
// 判断是否有索引层,
while (node.up !=null){
node.up.left.right = node.up.right;
node.up.right.left = node.up.left;
node = node.up;
}
}对于有序链表来说,时间复杂度为O(n),我们将链表改造成跳表之后,时间复杂度为多少呢?首先来分析对于有n个节点的链表,需要建立多少级索引?如果我们每两个节点会提取一个节点作为一个索引节点,那么第一级索引节点的个数为n/2,第二级索引节点的个数为n/4,依此类推,则第K级的索引节点的个数为n/(2^k)。
假设索引有h级,且第h级的索引节点个数为2,如下图所示。则我们可以得出n/(2^h)=2,这样可以得到h=logn-1(这里的log是指以2为底),加上链表本身的一层,则整个跳表的高度为logn。我们在跳表中查询某个数据时,如果每一层都需要遍历m个节点,那么在跳表中查询某个数的时间复杂度为O(m*log(n))。
比起单纯的单链表,跳表需要存储多级索引,肯定要消耗更多的存储空间。我们来看看跳表的空间复杂度,假设原始链表大小为 n,每两个元素直接提取一个索引,那第一级索引大约有 n/2 个结点,第二级索引大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下 2 个结点。如果我们把每层索引的结点数写出来,就是一个等比数列。这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。
以上就是跳表相关的知识,我使用双向链表来实现跳表,相对来说能够更好的理解跳表的思想,在使用是用单链表实现就可以了,单链表比双链表节约空间。
示例代码:GitHub
如果您发现文中错误,还请多多指教。欢迎关注个人公众号,一起交流学习。

标签:空间 ble 现在 tps 分析 java null 使用 byte
原文地址:https://www.cnblogs.com/jamaler/p/11397338.html