标签:http dup 二分查找 tor 现在 fibonacci click void 切分
18:35:51 2019-08-23
学习
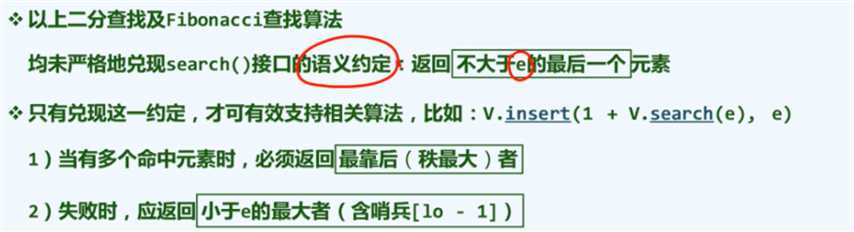
无序向量的操作 以及 有序向量 二分查找 Fibonacci查找

1 #define _CRT_SECURE_NO_WARNINGS //vs中scanf为不安全的函数 要使用 得加上这句话 2 #include<stdio.h> 3 #define Size 10 4 int Vector[10] = { 1,6,8,9,11,15,18,33,40,61 }; 5 //int Vector[Size]; 6 // 无序向量 7 int GetElement(int Rank) //按秩访问元素 8 { 9 if (Rank < Size) 10 return Vector[Rank]; 11 else 12 return -1; 13 } 14 void Insert(int Rank, int Element) //按秩插入元素 15 { 16 if (Rank < Size) 17 { 18 for (int i = Size - 1; i >Rank; i--) 19 { 20 Vector[i] = Vector[i - 1]; 21 } 22 Vector[Rank] = Element; 23 } 24 } 25 int Delete(int lo, int hi) //区间删除 单元素删除时区间删除的特列 26 { 27 for (;hi< Size;) 28 Vector[lo++] = Vector[hi++]; 29 return hi - lo; 30 } 31 int Find(int Element,int lo,int hi) //在范围中查找元素 32 { 33 while (lo<hi-- && Vector[hi] != Element); 34 return hi; 35 } 36 int DeleteOne(int Rank) //单元素删除 37 { 38 Delete(Rank, Rank + 1); 39 return Vector[Rank]; 40 } 41 void DeDuplicate() //无序向量的唯一化 低效版 42 { 43 int i = 0; 44 while (i<Size) 45 { 46 Find(Vector[i], 0, i) > 0 ? DeleteOne(i) : i++; 47 } 48 } 49 50 51 //有序向量 52 void LowDuplicate() // 有序向量的唯一化 低效版 O(n^2) 53 { 54 int i = 0; 55 while (i<Size) 56 { 57 (Vector[i] == Vector[i + 1]) ? DeleteOne(i+1) : i++; 58 } 59 } 60 61 int HighDuplicate() //有序向量的唯一化 高效版 O(n) 62 { 63 /*int i = 0; 64 int j = 1; 65 while (i<Size) 66 { 67 if (Vector[i] == Vector[j]) 68 j++; 69 Delete(i + 1, j + 1); 70 i = j+1; 71 }*/ //错误写法 利用delete(lo,hi)并不能达到高效率 72 //直接从后面截取 73 int i = 0; 74 int j = 0; 75 while (j < Size) 76 { 77 if (Vector[i] != Vector[j]) 78 Vector[++i] = Vector[j]; 79 else 80 j++; 81 } 82 //int size = ++i; shrink(); //直接删除掉尾部的多余元素 83 return j - i;// 返回删除元素总数 84 /*上面这个可写成 85 int i=0,j=0; 86 while(++j<size) 87 { 88 if(Vector[i]!=Vector[j]) 89 Vector[++i]=Vector[j]; 90 } 91 */ 92 } 93 94 //二分查找 O(LogN) //减而治之 95 //下面三个版本A 96 /*int BinarySearch(int Element, int lo, int hi) //二分查找1 对特殊情况未做处理 //左右转向代价不平衡 97 { 98 while (lo<=hi) 99 { 100 int i = (lo + hi) / 2; 101 if (Element < Vector[i]) 102 hi = i-1; 103 else if(Element>Vector[i]) 104 lo = i+1; 105 else 106 return i; 107 } 108 return -1; 109 }*/ 110 /*int BinarySearch(int Element, int lo, int hi) //二分查找2 对特殊情况处理不够好 111 { 112 if (lo >= hi) 113 return hi; 114 int i = (lo + hi) / 2; 115 if (Element < Vector[i]) 116 return BinarySearch(Element, lo, i-1); 117 else if (Element > Vector[i]) 118 return BinarySearch(Element, i+1, hi); 119 else 120 return i; 121 }*/ 122 /*int BinarySearch(int Element, int lo, int hi) //二分查找3 邓公实现方式 我未完善 123 { 124 125 while (lo<hi) 126 { 127 int i = (lo + hi) >> 1; // 位运算比乘除法快 128 if (Element < Vector[i]) 129 hi = i; 130 else if (Vector[i] < Element) 131 lo = i + 1; 132 else 133 return i; 134 } 135 return -1; 136 }*/ //上面三个思路都是一样的 选取中间为切分点(轴点) 137 138 /*int BinarySearch(int Element, int lo, int hi) //版本B 二分查找改进版 将判断从三个改为两个 牺牲刚好命中节点的情况 来换取左右每次转向的代价平衡 139 { //相较于上面的版本 这种算法在最好(坏)的情况下更坏(好) 140 /*while (1<hi-lo) //各种情况下的SL(search length?)更加接近 整体性能趋于稳定 141 { 142 int i = (lo + hi) / 2; 143 if (Element < Vector[i]) 144 hi = i; 145 else 146 lo = i; 147 } 148 if (Element == Vector[lo]) 149 return lo; 150 else 151 return -1;*/ 152 //上面这个可写成 153 /*while(1 < hi - lo) 154 { 155 int i = (lo + hi)>>1; 156 (Element < Vector[i]) ? hi = i : lo = i; 157 } 158 return (Element == Vector[lo]) ? lo :-1; 159 }*/ 160 161 int BinarySearch(int Element, int lo, int hi) //版本C 满足了找到不大于元素Element的最大秩 162 { 163 while (lo<hi) 164 { 165 int i = (lo + hi) / 2; 166 (Element < Vector[i]) ? hi = i : lo = i + 1; //对于小于所有数组内值 的元素 i会变为0 167 //对于大于所有数组内值 的元素 i会变为Size 168 //对于大于某一部分数组内值 的元素 i最终会变为 该数组元素下标加一 169 } 170 return --lo; 171 } 172 173 //Fibonacci查找算法 //使向左的操作变多 向右的操作变少 O(logN) 174 //Fibonacci 查找的算法的 ASL(average searth length 平均查找长度) (在常数意义上)优于二分查找 175 void Fibonacci(int* F,int size) 176 { 177 F[0] = F[1] = 1; 178 for (int i = 2; i < size; i++) 179 F[i] = F[i - 1] + F[i - 2]; 180 } 181 /*int FibonacciSearch(int Element,int lo,int hi) //这个做法补全了元素 是得任意的数组都可以满足Fibonacc查找的条件 182 { 183 int fib[Size]; 184 Fibonacci(fib, Size); 185 int k = 0; 186 while (hi > fib[k]-1) //找到以个Fibonacc的元素使其减一后大于等于元素总数 187 k++; 188 for (int i = hi; hi < fib[k] - 1; i++) //补全数组 使数组依旧有序 189 Vector[i] = Vector[hi - 1]; 190 while (lo<hi) 191 { 192 int i = (lo + fib[k - 1] - 1); //选取的位置 193 if (Element < Vector[i]) 194 { 195 hi = i; 196 k -= 1; //在左侧的话减一 197 } 198 else if (Vector[i] < Element) 199 { 200 lo = i + 1; 201 k -= 2; //在右侧的话减二 202 } 203 else 204 return i; 205 } 206 return -1; 207 }*/ 208 int FibonacciSearch(int Element, int lo, int hi) //这个更加容易理解 利用切分点对有序向量进行划分 209 { //利用Fibonacc数列分割 使得每次向左操作数多一点 因为向左只需要比较一次 210 int fib[Size]; 211 Fibonacci(fib, Size); 212 int k = 19; 213 while (lo<hi) 214 { 215 while (hi - lo < fib[k]) //找到一个Fibonacc数列某个元素使其 尽可能刚好小于 数组元素总数 216 k--; //这就是不断找到可以用来分割 数组的 Fibonacc数列的元素 217 int i = lo + fib[k] - 1; 218 if (Element < Vector[i]) 219 hi = i; 220 else if (Vector[i] < Element) 221 lo = i + 1; 222 else 223 return i; 224 } 225 return -1; 226 227 } 228 int main() 229 { 230 for (int i = 0; i < Size; i++) 231 { 232 printf("%d ", Vector[i]); 233 } 234 printf("\n"); 235 int Element=0; 236 while(scanf("%d", &Element)) 237 printf("%d\n",BinarySearch(Element, 0, Size)); //二分查找 238 /*for (int i = 0; i < 7; i++) 239 { 240 printf("%d ", Vector[i]); 241 } 242 int Element = 0; 243 printf("\n"); 244 while (scanf("%d", &Element)) 245 printf("%d\n", FibonacciSearch(Element, 0, 7)); //Fibonacc查找 */ 246 }
以前写代码时写注释写的少 。。导致现在注释写的很难看。。。。

标签:http dup 二分查找 tor 现在 fibonacci click void 切分
原文地址:https://www.cnblogs.com/57one/p/11402573.html