图的3种储存方式

标签：scan   编号   比较   最大   查找   art   pre   部分   color   

   图的储存方式有三种

一。邻接矩阵　　

　　优点：简洁明了，调用方便，简单易写；

　　缺点：内存占用大，而且没办法存重边（可能可以，但我不会），点的个数超过 3000 直接爆炸

　　适用范围：点的个数少，稠密图，一般结合floyed使用，可以传递闭包。

　　代码：

    scanf("%d%d",&u,&v,&w);
    a[u][v]=w;
    a[v][u]=w;// 双向边

二。邻接表

　　优点：占用空间小，可以快速查找每个点的出度，重边可以存，写着较为方便

　　缺点：查找和删除边很不方便，对于无向图，如果需要删除一条边，就需要在两个链表上查找并删除，用了STL，速度会慢

　　适用范围：大部分情况，不要求删除边就行

　　代码：

struct Edge{
    int v,w;
};
vector <Edge> edge[maxn];
void addedge(int u,int v,int w)
{
    edge[u].push_back({v,w});
    edge[v].push_back({u,w});//双向边
}

三。链式前向星

　　优点：比邻接表还省空间，可以解决某些卡空间的问题，删除边也很方便，只需要更改next指针的指向即可，速度也快

　　缺点：好像就是写的麻烦，理解麻烦，性能好像很猛

　　适用：需要删除边的题目，速度时间都要求高的题目

　　代码：

struct Edge{
    int to,w,next;
}edge[maxn*2];
int cnt,head[maxn],s,t,n,m;
void addedge(int u,int v,int w)
{
    edge[++cnt].to=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=top;
}
struct Pre{
    int v,edge;
}pre[maxn];

 　　解释:这是比较难理解的一种方式,所以做一下解释,主要是看别人的博客看懂的

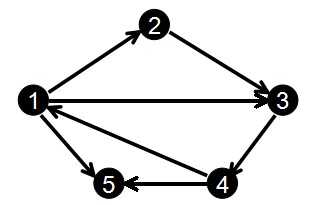
　　对于上图,输入为

　　1 2

　　2 3

　　3 4

　　1 3

　　4 1

　　1 5

　　4 5

　　对于上面的结构体，　　其中edge[i].to表示第i条边的终点　　,edge[i].next表示与第i条边同起点的下一条边的存储位置,　　edge[i].w为边权值.

　　数组head[],它是用来表示以i为起点的第一条边存储的位置,　head[]数组一般初始化为-1　实际上你会发现这里的第一条边存储的位置其实在以i为起点的所有边的最后输入的那个编号.

　　有了以i为起点的第一条边的储存位置和同起点下一条边的储存位置我们就可以便利这个i点的每一条边了

　　初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

　　edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

　　edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

　　edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

　　edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

　　edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

　　edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

　　edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

　　很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

 　　这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.

　　比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5   而head[1] = 5

　　我们在遍历以u节点为起始位置的所有边的时候是这样的:

　　for(int i=head[u];~i;i=edge[i].next)

　　那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也就是编号0的边,可以看出是逆序的.

第三部分引用了https://blog.csdn.net/ACdreamers/article/details/16902023 感谢原作者

图的3种储存方式

标签：scan   编号   比较   最大   查找   art   pre   部分   color   

原文地址：https://www.cnblogs.com/ztdf123/p/11391062.html