Leetcode solution 124: Binary Tree Maximum Path Sum

标签：cape   one   note   tail   global   lob   tput   math   leetcode   

 Problem Statement 

Input: [1,2,3]

       1
      /      2   3

Output: 6

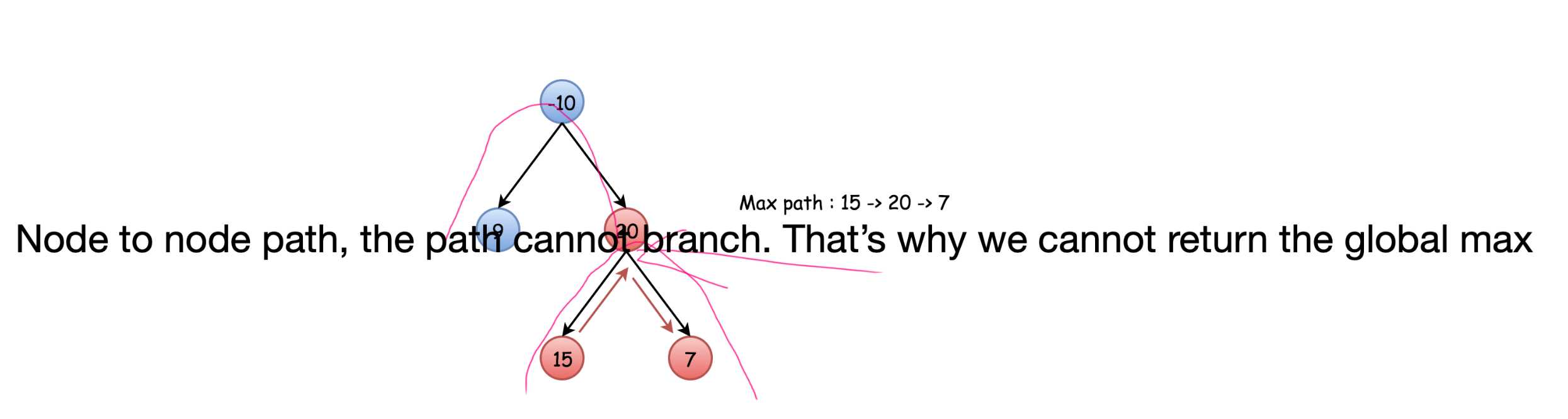
Input: [-10,9,20,null,null,15,7]

   -10
   /   9  20
    /     15   7

Output: 42

Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

When dealing with binary tree related problem, traversals using recursion is our friend. It seems we can perform a post-order traversal, and keep track of the maximum sums.

If the path has to go through root, then in each post-order step, we will have the max_sum_of_the_left_path, max_sum_of_the_right_path, the current_node_value, we simply return and record

single_path_max = max(the current_node_value, max(max_sum_of_the_left_path, max_sum_of_the_right_path) + current_node_value)

However, the problem allows a path that not goes through the root, therefore, we need to also record a max between left + current node value + right, i.e.,

global_max = max(single_path_max, max_sum_of_the_left_path + current_node_value + max_sum_of_the_right_path)

One caveat is in your recursion, we should still return the single_path_max. The reason we should not return the global_max is in that case, it will not be a single node to single node path.

Solutions

Post-order recursion

 1 private int max = Integer.MIN_VALUE;
 2 
 3 public int maxPathSum(TreeNode root) {
 4     maxPathSumHelper(root);
 5     return this.max;
 6 }
 7 
 8 public int maxPathSumHelper(TreeNode root) {
 9     if (root == null) {
10         return 0;
11     }
12 
13     int left = maxPathSumHelper(root.left);
14     int right = maxPathSumHelper(root.right);
15 
16     // the max on a single path
17     int singlePath = Math.max(root.val, Math.max(left, right) + root.val);
18     // max across the current node on two sides
19     int acrossPath = Math.max(singlePath, left + right + root.val);
20     if (acrossPath > this.max) {
21         this.max = acrossPath;
22     }
23 
24     // Note: always want to return the single path for recursion, because you cannot include both path, else,
25     // it will not be a path
26     return singlePath;
27 }

 Time Complexity: O(N), each node is visited once

Space Complexity:No extra space is needed other than the recursion function stack

References

• Leetcode official solution

Leetcode solution 124: Binary Tree Maximum Path Sum

标签：cape   one   note   tail   global   lob   tput   math   leetcode   

原文地址：https://www.cnblogs.com/baozitraining/p/11404552.html