小A的数学题

标签：-o   pre   正整数   表示   one   event   com   pen   span   

小A最近开始研究数论题了，这一次他随手写出来一个式子，

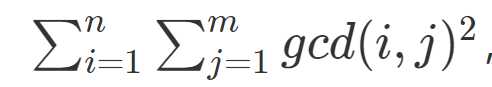
但是他发现他并不太会计算这个式子，你可以告诉他这个结果吗，答案可能会比较大，请模上1000000007。

输入描述:

一行两个正整数n，m一行两个正整数n，m一行两个正整数n，m

输出描述:

一行一个整数表示输出结果一行一个整数表示输出结果一行一个整数表示输出结果

2 2

7

备注1≤n,m≤1e61 \leq n,m \leq 1e61≤n题意：给定两个数，n,m;求（1~n）（1~m)的 gcd(i,j)平方和

思路：简单暴力肯定超时， 
看两个数的最大公约数，我们反过来求，从min(n,m)最大的可能公约数开始逐级递减
从min(n,m)~1
令 p = min(n,m),
那么在n里面p的倍数有n/p个，即有n/p个数存在p这个约数
对于m而言也一样；
之后再从 p*2开始将所有p的倍数再减掉，剩下的就是约数最大为p的个数，即对于n,m而言就是gcd(n,m)==p的所有组合为（n/p)*(m/p);

例子
 n = 9, m= 7;
p = 7;
gcd(i,j) == 7;
f[7] = 1;
gcd(i,j)=6;
f[6]=1;
gcd(i,j) = 5;
f[5]=5;
gcd(i,j)=4;
 f[4]=2；

gcd(i,j)=3;
f[3]=5;

gcd(i,j)=2;
f[2]=9;
f[1]=44;

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 typedef long long ll;
 5 const int N = 1e6+10;
 6 #define mod 1000000007
 7 ll n,m;
 8 ll num;
 9 ll f[N];
10 int main()
11 {
12     scanf("%lld%lld",&n,&m);
13     for(int i = min(n,m); i >=1;i--)
14     {
15         f[i] = (n / i) * (m / i);
16         for(int j = 2 * i; j <= min(n , m); j += i)
17         {
18             f[i] -= f[j];
19         }
20         //cout << f[i]<<‘ ‘<<i<<endl;
21         num = (num + f[i] * i % mod * i % mod )%mod;
22     }
23     cout << num <<endl;
24     return 0;
25 }

View Code

小A的数学题

标签：-o   pre   正整数   表示   one   event   com   pen   span   

原文地址：https://www.cnblogs.com/wangzhe52xia/p/11404406.html