标签:cout mes font sed 使用 res struct 而且 线段
T1 jigsaw

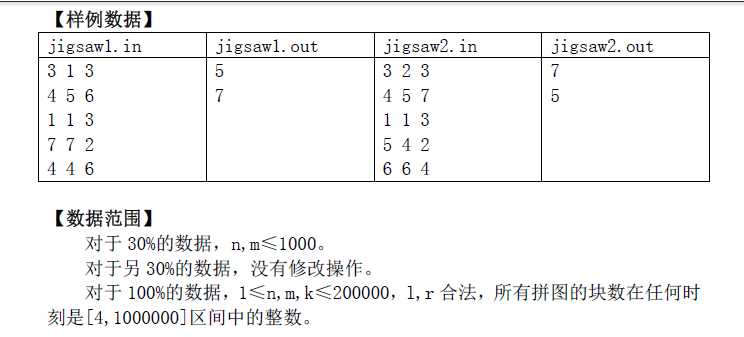
一开始看到这题的时候,这么多区间询问,修改,想到会用某种数据结构来维护,而且每次喊你异或上一次的答案,肯定是强制在线,这时就听到诸如树套树之类的神仙解法,但本sb蒟蒻并不会,就敲了个sb暴力线段树。原想到树套树肯定是本题正解,但实际上本题正解非常的不可思议。
先观察一下,答案都是在4-1000000之间的质数,所以肯定都是奇数,而每次都要异或答案,结果只能为1或2。所以我们可以反过来想,如果opt为奇数,那么肯定答案异或上奇数的最后一位是0,所以可以让操作符异或上2就是答案。反之,opt是偶数时就异或上1。有了这个思路这题分分钟的事情。这下一直处理到最后一个询问。暴力就可以了!
真的巧妙,积累在这里。

//这题思路是真的强!!! #include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; int prime[maxn]; int a[maxn],n,m,k; int last; int opt,l,r; int ans[maxn]; int tot; int vis[maxn]; int isprime[maxn]; int kkk; bool flag; void check(int n){ memset(vis,0,sizeof(vis)); for(int i=2;i<=n;i++){ if(!vis[i]){ vis[i]=i; prime[++kkk]=i; } for(int j=1;j<=kkk;j++){ if(prime[j]>vis[i]||prime[j]>n/i) break; vis[i*prime[j]]=prime[j]; } } for(int i=1;i<=kkk;i++) isprime[prime[i]]=true; } int main(){ freopen("jigsaw.in","r",stdin); freopen("jigsaw.out","w",stdout); scanf("%d%d%d",&n,&k,&m); for(register int i=1;i<=n;i++) scanf("%d",&a[i]); check(1000000); for(register int i=1;i<=m;i++){ scanf("%d%d%d",&opt,&l,&r); if(flag){ if(opt%2==1) last=opt^2;//因为lastans为4-1000000中的质数都是奇数,二进制末位为1,可以根据这个性质得出答案 else last=opt^1; flag=false; printf("%d\n",last); } l^=last,r^=last,opt^=last; if(opt==1) flag=true; else a[l]=r; } if(opt==1){//最后一个询问暴力改 for(int i=l;i<=r;i++) if(isprime[a[i]]) ans[++tot]=a[i]; sort(ans+1,ans+1+tot); printf("%d\n",ans[k]); return 0; } return 0; }
T2 T3就不说了,真的是神仙题,先把std放在这里,之后再来填坑.
T2 baritone
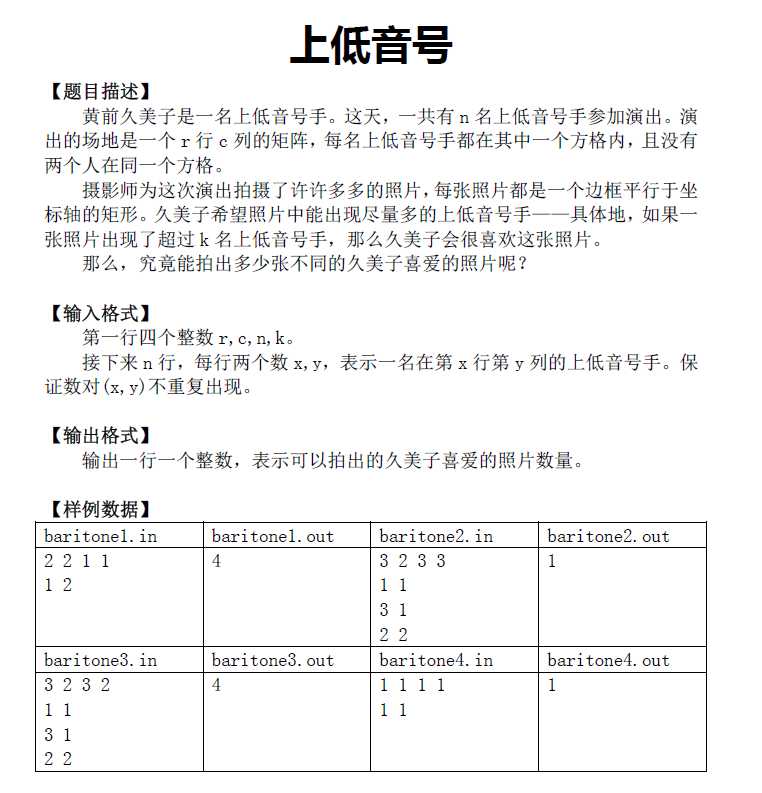
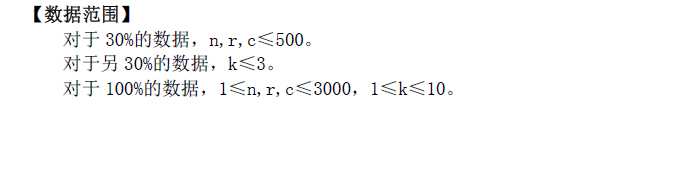
题解如下:
从上往下枚举上边界,从下往上枚举下边界。考虑已经统计出上下边界为枚举的包含至少k个点的矩形数,当下边界往上移动时,可能会删除某些点。用按横坐标排序的有序表维护当前上下边界间的点,只有删除点的前k个点和后k个点会影响答案,其它矩形区域依然可行。这样每次只需要从有序表中删除一个点并统计答案,使用链表即可。
复杂度O(n^2*k)
code:

#include <cstring> #include <algorithm> #include <cstdlib> #include <utility> #include <vector> #include <iostream> #include <set> #include <map> #include <queue> #include <functional> #include <numeric> #include <iomanip> #include <string> #include <sstream> #include <cmath> #include <ctime> using namespace std; const int xx[4] = {0, 1, 0, -1}; const int yy[4] = {1, 0, -1, 0}; const int maxn = 4000; int r, c, n, k, len, x[maxn], y[maxn]; int ne[maxn], pr[maxn], val[maxn], tx[maxn]; int que[maxn], to[maxn], f[maxn]; long long ans, sum; vector <int> ve[maxn]; char getc() { char c = getchar(); while (c <= 32) c = getchar(); return c; } bool cmp(int x, int y) { if (que[x] != que[y]) return que[x] < que[y]; else return f[x] < f[y]; } void del(int t) { ne[pr[t]] = ne[t]; pr[ne[t]] = pr[t]; sum -= val[t]; int x = ne[t], y = ne[t]; for (int i = 1; i < k; i++) y = ne[y]; for (int i = 1; i <= k + 1; i++) { int v = (que[x] - que[pr[x]]) * (r - que[y] + 1); sum += v - val[x]; val[x] = v; x = pr[x]; y = pr[y]; } } int main() { freopen("baritone.in", "r", stdin); freopen("baritone.out", "w", stdout); scanf("%d%d%d%d", &r, &c, &n, &k); ans = 0; for (int i = 1; i <= n; i++) scanf("%d%d", &x[i], &y[i]), ve[y[i]].push_back(i); for (int i = 1; i <= c; i++) { sum = 0; len = 0; for (int j = 0; j <= 20; j++) que[++len] = 0, que[++len] = r + 1; for (int j = 1; j <= n; j++) if (y[j] >= i) { que[++len] = x[j]; f[len] = y[j]; to[j] = len; } for (int j = 1; j <= len; j++) tx[j] = j; sort(tx + 1, tx + len + 1, cmp); for (int j = 1; j < len; j++) ne[tx[j]] = tx[j + 1], pr[tx[j + 1]] = tx[j]; ne[tx[len]] = tx[len]; pr[tx[1]] = tx[1]; for (int j = 1; j <= len; j++) { int now = j; for (int p = 1; p < k; p++) now = ne[now]; val[j] = (que[j] - que[pr[j]]) * (r - que[now] + 1); sum += val[j]; } for (int j = c; j >= i; j--) { ans += sum; for (int p = 0; p < (int) ve[j].size(); p++) del(to[ve[j][p]]); } } cout << ans << endl; return 0; }
T3 coffee

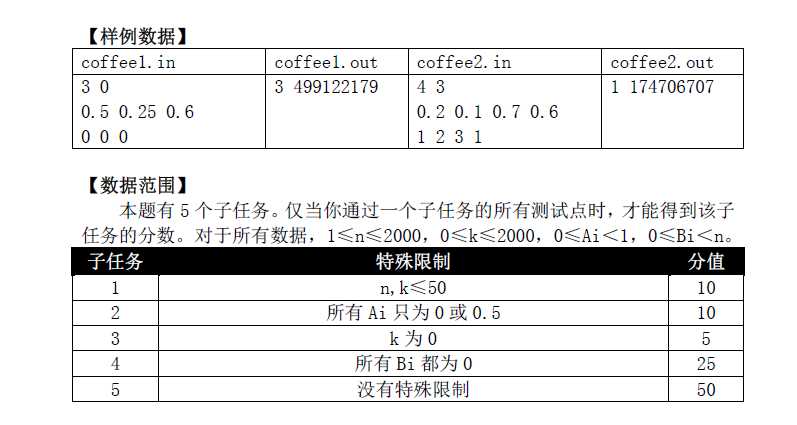

这题更神仙,题解搬运如下:
考虑使用dp解决这个问题。用表示使用i次能力,当前有一罐j种咖啡,期望能喝到多少罐,则
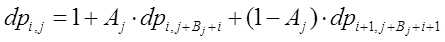
发现dp时会产生环,则记忆化搜索并记录当前项的系数,在发现环后根据当前系数解出环上的dp值。为了输出取模后的值,需要实数dp一次,取模后再dp一次,根据实数dp的结果找到最优解的位置,再输出取模dp的答案即可。
%%%%% code:

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <cassert> #include <cmath> using namespace std; typedef long long LL; const int maxn=2010, mod=998244353; const double eps=1e-12; int n, k; LL qpow(LL num, int cnt=mod-2){ LL back=1; for (; cnt; cnt>>=1){ if (cnt&1) back=back*num%mod; num=num*num%mod; } return back; } struct Value{ double val; int mval; Value (int numerator=-1, int denominator=1){ mval=qpow(denominator)*numerator%mod; val=(double)numerator/denominator; } inline Value operator * (const Value &an){ Value back; back.val=val*an.val; back.mval=(LL)mval*an.mval%mod; return back; } inline Value operator / (const Value &an){ Value back; if (fabs(val)<eps) back.val=0; else back.val=val/an.val; back.mval=qpow(an.mval)*mval%mod; return back; } inline Value operator + (const Value &an){ Value back; back.val=val+an.val; back.mval=(mval+an.mval)%mod; return back; } inline Value operator - (const Value &an){ Value back; back.val=val-an.val; back.mval=(mval-an.mval+mod)%mod; return back; } inline bool valid(){ return ~mval; } void read(){ cin>>val; mval=(int)(val*1000+0.5)*qpow(1000)%mod; } }; ostream &operator << (ostream &os, const Value &an){ os<<an.val<<" / "<<an.mval; return os; } Value _1=Value(1,1), _0=Value(0,1); struct state{ Value k, v; state(Value k=_1, Value v=_0):k(k), v(v){} state add(Value k2, Value v2){ return state(k*k2, k*v2+v); } } nil; class costumStack{ private: state sta[maxn]; int siz; public: void push(state an){ sta[++siz]=an; } int size(){ return siz; } void pop(){ siz--; } state top(){ return sta[siz]; } state get(int pos){ return sta[pos]; } } sta; Value dp[maxn][maxn]; Value a[maxn]; int b[maxn]; int dep[maxn]; int maxcycle; Value get(int x, int y, state s=nil, int layer=1){ while (y>n) y-=n; if (dp[x][y].valid()) return dp[x][y]; if (dep[y]){ state tmp=sta.get(dep[y]); // cerr<<"["<<x<<","<<y<<", cycle: "<<layer-dep[y]<<"] "<<s.k<<" "<<s.v<<endl; maxcycle=max(maxcycle, layer-dep[y]); tmp.k=tmp.k-s.k; tmp.v=s.v-tmp.v; return dp[x][y]=tmp.v/tmp.k; } dep[y]=layer; sta.push(s); int tmp=y+b[y]+x; Value tmpv=(_1-a[y])*get(x+1, tmp+1)+_1; dp[x][y]=a[y]*(get(x, tmp, s.add(a[y], tmpv), layer+1))+tmpv; sta.pop(); dep[y]=0; return dp[x][y]; } int main(){ freopen("coffee.in", "r", stdin); freopen("coffee.out", "w", stdout); cin>>n>>k; int maxpos=0; for (int i=1; i<=n; i++){ a[i].read(); if (a[i].val>a[maxpos].val) maxpos=i; } for (int i=1; i<=n; i++) cin>>b[i]; for (int i=1; i<=n; i++) dp[k+1][i]=_0; for (int i=k; i>=0; i--){ // cout<<i<<endl; for (int j=1; j<=n; j++) get(i, j); } // for (int j=0; j<=k; j++) // for (int i=1; i<=n; i++) // cerr<<"Case "<<j<<","<<i<<" : "<<dp[j][i]<<endl; double mindif=1e20; double maxans=0; int pos=0; for (int i=1; i<=n; i++){ if (!pos||dp[0][i].val>maxans){ pos=i; mindif=dp[0][i].val-maxans; maxans=dp[0][i].val; } else { mindif=min(mindif, maxans-dp[0][i].val); } } /* cerr<<"Minimum difference is: "<<mindif<<endl; cerr<<"Maxpos = "<<maxpos<<", ans = "<<pos<<endl; FILE *fres=fopen("res.txt", "w"); if (mindif<1e-4||k&&maxcycle<(n/10)){ fprintf(fres, "Invalid"); } else { fprintf(fres, "OK"); }*/ printf("%d %d\n", pos, dp[0][pos].mval); return 0; }
复杂度O(n*k)
标签:cout mes font sed 使用 res struct 而且 线段
原文地址:https://www.cnblogs.com/LJB666/p/11405777.html