定心,规范化,白化

标签：lin   span   重要   协方差矩阵   end   lock   偏差   通过   info   

输入定心

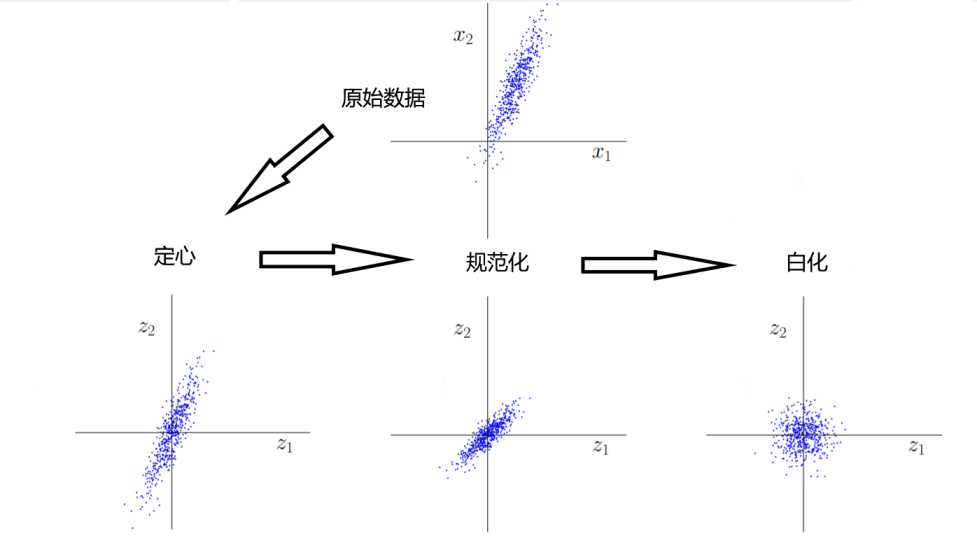
定心是通过更改输入\(\mathtt{X}\)的原点移除输入中的偏差,即使得变换后的输入\(\mathtt{Z}\)均值为零

输入的平均值\(\bar{\mathtt{x}}=\frac{1}{N}\mathtt{X^T1}\)

• \[\mathtt x=\begin{bmatrix} {x_0}\ {x_1}\ {\vdots}\ {x_d}\ \end{bmatrix}\] \(\mathtt x\in R^{(d+1)*1}\)
• \[\mathtt{X}=\begin{bmatrix}{\mathtt{x_1^T}}\\{\mathtt{x_2^T}}\\{\vdots}\\{\mathtt{x_N^T}}\\\end{bmatrix}\] \(\mathtt X\in R^{N*(d+1)}\)
• \(\mathtt{1}=\begin{bmatrix}{1}\\{1}\\{\vdots}\\{1}\\\end{bmatrix}\) \(\mathtt 1\in R^{N*1}\)

转换后的输入\(\mathtt{z_n=x_n-\bar{x}}\)

或者\(\mathtt{Z=X-1\bar{x}^T}\)

证明变换后输入均值为零

\(\mathtt{\bar{z}=\frac{1}{N}Z^T1=\frac{1}{N}X^T1-\frac{1}{N}\bar{x}1^T1=\bar{x}-\frac{1}{N}\bar{x}N}=0\)

输入规范化

定心是通过对输入\(\mathtt{X}\)进行特征缩放,使得变换后的输入\(\mathtt{Z}\)每个特征标准差为1

以下讨论建立在定心的基础上

标准差计算方法\(\sigma=\sqrt{\frac{1}{N}\sum_{n=1}^N(x_{i}-\bar{x})^2}\),由于已经定心(\(\bar{x}=0\)),所以\(\sigma=\sqrt{\frac{1}{N}\sum_{n=1}^Nx_{i}^2}\)

标准差\(\sigma_i=\sqrt{\frac{1}{N}\sum_{n=1}^Nx_{ni}^2}\)

变换后\(\mathtt{z_n}=\begin{bmatrix}{x_{n1}/\sigma_1}\\{\vdots}\\{x_{nd}/\sigma_d}\\\end{bmatrix}=\mathtt{Dx_n}\)

• D是对角矩阵,\(\mathtt{D}_{ii}=1/\sigma_i\)

或者\(\mathtt{Z=XD}\)

证明变换后标准差为1

\(\sigma_i(\mathtt{z})=\sqrt{\frac{1}{N}\sum_{n=1}^Nz_{ni}^2}=\sqrt{\frac{1}{N}\sum_{n=1}^N\frac{x_{ni}^2}{\sigma_i^2}}=\sqrt{\frac{1}{\sigma_i^2}*(\frac{1}{N}\sum_{n=1}^Nx_{ni}^2)}=1\)

输入白化

如果输入特征之间相关性较高,那么在做正则化时对不同特征的独立惩罚就很难做到,白化的作用就是减少特征间的相关性,同时使得所有特征具有相同的方差

白化是使得输入每个维度相同重要,降维是衡量输入维度的重要性然后舍弃不重要的维度,所以降维不应该在白化之后

以下讨论建立在定心的基础上

协方差矩阵\(\mathtt{C=\frac{1}{N}\sum_{n=1}^{N}x_nx_n^T}=\frac{1}{N}X^TX\)

• \(C_{ij}=cov(x_i,x_j)\) 该协方差描述了\(x_i\)和\(x_j\)的相关性
• \(cov(x,y)=E(xy)-E(x)E(y)=E(xy)\)这里已经定心过,所以\(E(x)=E(y)=0\)
• \(\mathtt{x_nx_n^T}=\begin{bmatrix}{x_1x_1}&{x_1x_2}&{\cdots}&{x_2x_d}\\{x_2x_1}&{x_2x_2}&{\cdots}&{x_2x_d}\\{\vdots}&{\vdots}&{\ddots}&{\vdots}\\{x_dx_1}&{x_dx_2}&{\cdots}&{x_dx_d}\\\end{bmatrix}\) 这下看懂了吧

转换后输入\(\mathtt{z_n=C^{-\frac{1}{2}}x_n}\)(这里矩阵的开方我也不是很懂)

或者\(\mathtt{Z=XC^{\frac{1}{2}}}\)

白化后的输入的协方差矩阵

\(\mathtt{\frac{1}{N}Z^TZ=C^{-\frac{1}{2}}(\frac{1}{N}X^TX)C^{-\frac{1}{2}}=C^{-\frac{1}{2}}CC^{-\frac{1}{2}}=(C^{-\frac{1}{2}}C^{\frac{1}{2}})(C^{\frac{1}{2}}C^{-\frac{1}{2}})=E}\)

最后得到一个单位矩阵,即\(cov(x_i,x_j)=\begin{cases}1,i=j\\0,i\neq{j}\end{cases}\),这说明每个输入特征只与自身相关,与其它特征不相关

图示

定心,规范化,白化

标签：lin   span   重要   协方差矩阵   end   lock   偏差   通过   info   

原文地址：https://www.cnblogs.com/redo19990701/p/11407115.html