线段树

标签：个数   直接   信息   假设   连续   提高   效率   下标   src   

线段树

线段树的由来

一般来说，对于[1,n]的操作，修改与统计，复杂度是O(n)，但是用先单数优化，可以达到O(log(n))
比如

题目一：
10000个正整数，编号1到10000，用A[1],A[2],A[10000]表示。
修改：无
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.

方法一:对于统计L,R ，需要求下标从L到R的所有数的和，从L到R的所有下标记做[L..R],问题就是对A[L..R]进行求和。
这样求和，对于每个询问，需要将(R-L+1)个数相加。
方法二:更快的方法是求前缀和,令 S[0]=0, S[k]=A[1..k] ，那么，A[L..R]的和就等于S[R]-S[L-1]，
这样，对于每个询问，就只需要做一次减法，大大提高效率。

题目二：
10000个正整数，编号从1到10000，用A[1],A[2],A[10000]表示。
修改：1.将第L个数增加C （1 <= L <= 10000）
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.

方法一:直接修改第L个数
方法二:把L到R的所有值都要加上C

所以，从上面可以看出来，普通的方法对于修改比较快，但求和比较慢。前缀和求和比较快，但修改比较慢
所以，基于此问题，将修改和统计集与一体的线段树就诞生了

线段树介绍

线段树是一种二叉树结构，对于一个线段或区间，可以用一个二叉树来表示

假设有编号1到n的n个点，每个点都存了一些信息，用[L,R]来表示下标从L到R的这些点
线段树的作用就是，对编号连续的一些点进行修改或者统计操作，修改和统计的复杂度都是O(log(n))

如何划分区间

对于区间[1,n]分成不超过4n个子区间，对于每个子区间，记录一段连续数字的和，
知乎，任意给定区间[L,R],线段树再上述子区间种选择约2log(R-L+1)个拼成区间[L,R]
如果对于A[L]+=C的操作，线段树的子区间里，越有log(n)个包含了L，所以只需要修改log(n)个子区间

首先是讲原始子区间的分解，假定给定区间[L,R]，只要L < R ，线段树就会把它继续分裂成两个区间。
首先计算 M = (L+R)/2，左子区间为[L,M]，右子区间为[M+1,R]，然后如果子区间不满足条件就递归分解。
以区间[1..13]的分解为例，分解结果见下图

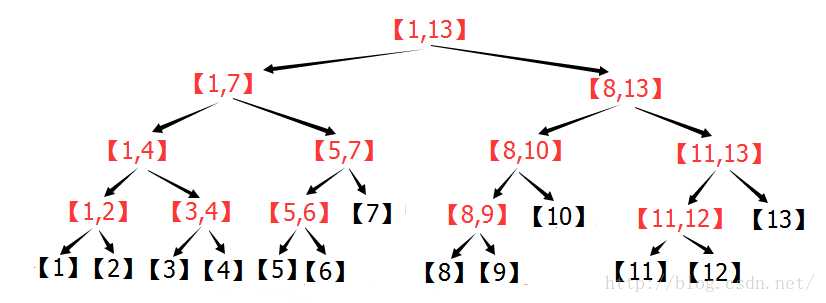
对于[2,12]呢

如何统计区间

假设这13个数为1,2,3,4,1,2,3,4,1,2,3,4,1. 在区间之后标上该区间的数字之和：

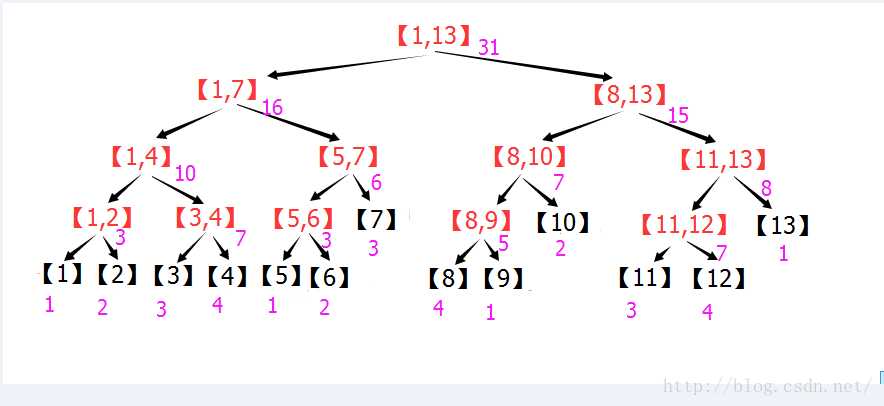
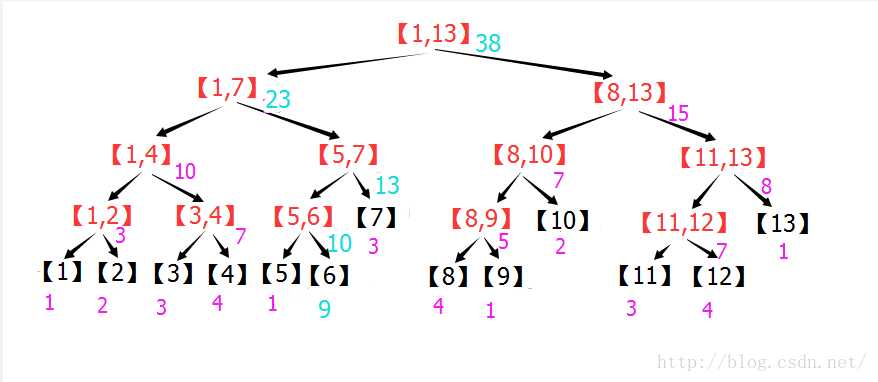
如果要计算[2,12]
[2,12]=[2]+[3,4]+[5.7]+[8,10]+[11,12]=29

如何点修改

线段树

标签：个数   直接   信息   假设   连续   提高   效率   下标   src   

原文地址：https://www.cnblogs.com/Emcikem/p/11412298.html