标签:color eth src 改变 class chess open one exist
Klein四元群$K$是满足下列乘法表的群
Klein four-group is the group satisfying the following multpilicative table
$$\begin{array}{|c|c|c|c|c|}\hline \cdot & 1 & a & b & c \\ \hline 1 & 1& a & b & c \\ \hline a & a & 1 & c & b \\ \hline b & b & c & 1 & a \\ \hline c & c & b & a & 1 \\ \hline \end{array}$$
显然,$K\cong \mathbb{Z}/2\times \mathbb{Z}/2$,这是最小的非循环群。
Clearly, $K\cong \mathbb{Z}/2\times \mathbb{Z}/2$, which is the smallest non-cyclic group.
我们知道如下三个事实
We know the following three facts
毫无疑问,$K$的自同构群是第三个对称群$\mathfrak{S}_3$.
There is no doubt that the automorphism group is the 3rd symmatric group $\mathfrak{S}_3$.
Klein四元群的特征表是
The character table of Klein four group is
$$\begin{array}{|c|c|c|c|c|}\hline & 1 & a & b & c \\ \hline 1 & 1 & 1 & 1 & 1 \\ \hline \chi_a & 1 & 1 & -1 & -1 \\ \hline \chi_b & 1 & -1 & 1 & -1 \\ \hline \chi_c &1 & -1 & -1 & 1\\ \hline \end{array}$$
最小的忠实置换表示是$\{1, (12)(34), (13)(24), (14)(23)\}\subseteq \mathfrak{S}_4$.
The minimal faithful permutation representaion is $\{1, (12)(34), (13)(24), (14)(23)\}\subseteq \mathfrak{S}_4$.
上述皆可由由下述解释。考虑三维空间中以$(1,1,1), (1,-1,-1), (-1,1,-1),(-1,-,1,1)$为顶点正四面体,其中$a,b,c$在上面的作用分别是绕$x,y,z$轴旋转$180^\circ$. 这实际上给出所有正四面体的反射自同构。面的置换就是上面的忠实表示。
All of above can be summarized as follow. Consider the tetrahedron in 3D space whose vertices are $(1,1,1), (1,-1,-1), (-1,1,-1),(-1,-,1,1)$, where the action of $a$, $b$ and $c$ is the rotation of $180^\circ$ along axis $x$, $y$ and $z$ respectively. These actually give rise to all of the automorphisms of reflection of the tetrahedron. The permutation of faces is exactly the faithful representation above.
如图在这篇博文中所提到的,有红黄蓝三色绵羊各15, 19, 20只,如果两只不同颜色的棉羊相撞,那么他们合体成另一个颜色的一只绵羊。问最终会全变成哪种颜色的羊?
There are 15, 19 and 20 sheep of color red, yellow and blue respectively. If two sheep of distinct colors collide, then they will blend into one sheep in the other color. What kind of species will unify the farm at the end?
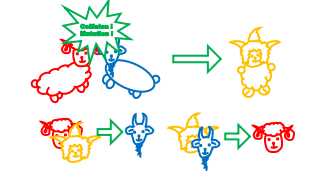
我们可以给出一个染色的方法,给三种颜色的绵羊染上Klein四元群中的$a,b,c$,那么相撞时,所有羊所染元素的乘积是不变的。
We can give a method through coloring---color three different kind of sheep with $a$, $b$ and $c$ in Klein four-group respectively. Then when collision happens, the product of elements colored is invariant.
而$15a+19b+20c=a+b=c$,所以最终是黄色的羊统一整个农场。
Note that 15a+19b+20c=a+b=c$, so the yellow sheep will unifty the whole farm.
考虑一个正八面体,我们在所有顶点上安装了一盏灯泡,在每个面上安装一个开关。每次使用开关,这个面的三个顶点的灯泡状态会发生改变——亮的灯被熄灭,熄灭的灯被点亮。如果现只有一盏灯亮着,我们能把所有灯关掉吗?
Consider a octahedron. We equip each vertice a bulb and each face a switch. Each usage of a switch, the three vertices of this face will change its state---the light one gets extincted, the light-off one turns off. Now there is only one bulb open, can we turn off all the bulbs?
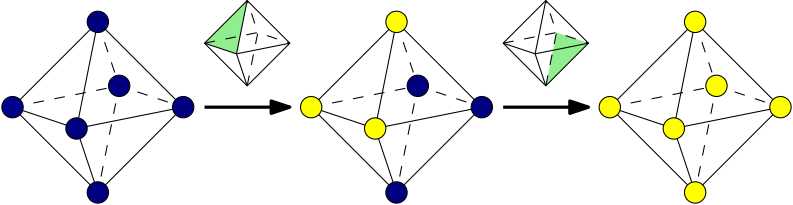
同样,我们给出一个染色的方法。将三组对径的顶点分别染上Klein四元群中的$a,b,c$,那么每次操作开关,所有亮的灯所染元素的乘积是不变的。
Similarly, we shall present a coloring solution. Coloring the three pairs of antipodal vertices with $a$, $b$ and $c$ in Klein four-group respectively. Then no matter how the switches are operated, the product of elements of light bulbs is invariant.
现在,只有一盏灯亮,当然没法变成都灭的状态。
Now, there is only one bulb on, it cannot become the state with all distinct.
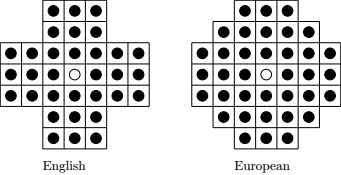
第三个应用是经典的,我们证明经典小游戏欧版的孔明棋(也称独立钻石)是无解的。
This application is classic. We will show that the game Peg Solitaire is unsolvable for European version.
给棋盘条带状染上Klein四元群中的$a,b,c$,每次跳子不会改变所有元素的乘积。
Coloring the board with $a$, $b$ and $c$ in Klein four-group in striped pattern. Each skip does change the product of all elements.
| a | b | c | ||||
| a | b | c | a | b | ||
| a | b | c | a | b | c | a |
| b | c | a | b | c | a | b |
| c | a | b | c | a | b | c |
| b | c | a | b | c | ||
| a | b | c |
现在,所有元素的乘积是$1$,说明不存在最终只有一个子的情况。
Now, the product is $1$. This shows that there does not exist the final state of only one chess.
[Bilingual]Klein四元群的三个例子Three examples of Klein four-group
标签:color eth src 改变 class chess open one exist
原文地址:https://www.cnblogs.com/XiongRuiMath/p/11415507.html