标签:正则 分类 each 代码 har char ima src 无法
这是一个基于等价类的算法。
split(S)
foreach char c
if c 能切分 S
split S into T1, T2, ..., TKhopcroft()
split all nodes into N, A(即非接收状态和接收状态)
while (set is still changing)
split(N/A)这里的等价类,通俗来说就是根据某些特征来划分状态。比如某些状态,都是接收状态,就可以被分为一类。某些状态都是非接收状态,它们就是一类。然后再看每一类中是否还可以继续被划分,比如某些状态经过一次转移可以到接收状态,有些状态不可以,那么这两种状态就是不同的,可以继续分类。
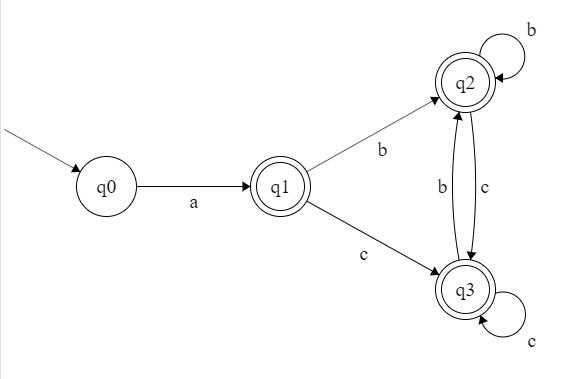
按照接收状态非接收状态划分,q0 单独一类,q1 q2 q3 是一类。因为 b 和 c 无法区分 q1 q2 q3 中的状态,所以这一个集合(q1, q2, q3)收缩成 q4。
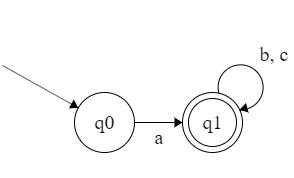
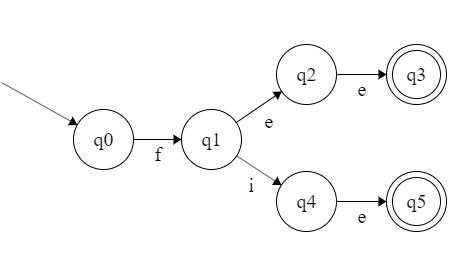
首先,{q0, q1, q2, q4} → N,{q3, q5} → A。
然后在 N 上看各个状态接收字符 e 之后的转移,q2 和 q4 都可以转移到 A 集合中,而 q0 和 q1 不行,所以再次分类:{q2, q4} → N1,{q0, q1} → N2。
在 N1 和 A 上看各个状态接收各个字符后的转移,发现无法继续划分,所以这就是一个最简状态集了。
在 N2 上看各个状态接收各个字符后的转移,发现接收字符 e 时,q1 可以转移到 N1,而 q0 不行。所以再次划分 N1:{q1} → N21,{q0} → N22。
再看各个状态集,都不可以被继续划分了。此时到达最简 DFA。
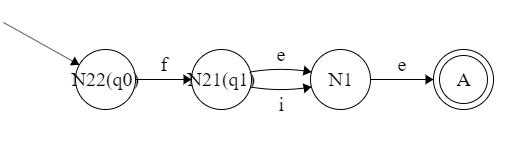
从正则表达式到 NFA 到 DFA 到最简 DFA (三)(结束)
标签:正则 分类 each 代码 har char ima src 无法
原文地址:https://www.cnblogs.com/metatronwings/p/11417473.html