标签:正交 简化 规格 高斯金字塔 不容易 关键点 优化 取出 node
参考尺度空间理论
当用一个机器视觉系统分析未知场景时,计算机没有办法预先知道图像中物体尺度,因此,我们需要同时考虑图像在多尺度下的描述,获知感兴趣物体的最佳尺度。所以在很多时候,我们会在将图像构建为一系列不同尺度的图像集,在不同的尺度中去检测我们感兴趣的特征。比如:在Harr特征检测人脸的时候,因为我们并不知道图像中人脸的尺寸,所以需要生成一个不同大小的图像组成的金字塔,扫描其中每一幅图像来寻找可能的人脸。
图像金字塔化的一般步骤:首先,图像经过一个低通滤波器进行平滑(这个步骤会使图像变模糊,好像模仿人的视觉中远处的物体没有近处的清晰的原理),然后,对这个平滑后的图像进行抽样(一般抽样比例在水平和竖直方向上都为1/2),从而得到一系列的缩小的图像。
数字图像的滤波可以简单的理解为:将图像中各个像素点的值变更为该像素点及其相邻区域像素点与一个滤波模板进行相乘后的值。图像金字塔中通常我们采用高斯模板对图像进行平滑。
高斯模板是如何生成的呢?
来看下opencv中的函数cv::getGaussianKernel()
\[G_i= \alpha *e^{-(i-( \texttt{ksize} -1)/2)^2/(2* \texttt{sigma}^2)},i=0,...,ksize-1 \]
\(\alpha\) 是尺度系数为了保证\(\sum_i G_i=1\), ksize就是模板的大小,模板通常是ksizeksize的矩形。使用这个函数我们得到的是ksize1的向量,由于gaussianBlur是一种可分离滤波器, 我们可以分别获取x方向和y方向的高斯核模板,先对行滤波,再对列滤波的方式进行滤波。
cv::GaussianBlur(blurred_image, blurred_image, cv::Size(7, 7), 2, 2, cv::BORDER_REFLECT_101);具体的计算分析可以看考手撕OpenCV源码之GaussianBlur

图像的金字塔化能高效地(计算效率也较高)对图像进行多尺度的表达,但它缺乏坚实的理论基础,不能分析图像中物体的各种尺度(虽然我们有小猫的金字塔图像,我们还是不知道原图像内小猫的大小)。
信号的尺度空间刚提出是就是通过一系列单参数、宽度递增的高斯滤波器将原始信号滤波得到到组低频信号。那么一个很明显的疑问是:除了高斯滤波之外,其他带有参数t的低通滤波器是否也可以用来生成一个尺度空间。
虽然很多研究者从可分性、旋转不变性、因果性等特性推出高斯滤波器是建立线性尺度空间的最优滤波器。然后在数字图像处理中,需要对核函数进行采样,离散的高斯函数并不满足连续高斯函数的的一些优良的性质。所以后来出现了一些非线性的滤波器组来建立尺度空间,如B样条核函数。
使用高斯滤波器对图像进行尺度空间金塔塔图的构建,让这个尺度空间具有下面的性质:
1)加权平均和有限孔径效应
信号在尺度t上的表达可以看成是原信号在空间上的一系列加权平均,权重就是具有不同尺度参数的高斯核。信号在尺度t上的表达也对应于用一个无方向性的孔径函数(特征长度为\(\sigma=\sqrt{t}\))来观测信号的结果。这时候信号中特征长度小于σ的精细结构会被抑制(理解为一维信号上小于σ的波动会被平滑掉)。
2)层叠平滑
也叫高斯核族的半群(Semi-Group)性质:两个高斯核的卷积等同于另外一个不同核参数的高斯核卷积。
\[g(\mu,\sigma_1)\ast g(\mu,\sigma_2)=g(\mu,\sqrt{\sigma_1^2+\sigma_2^2})\]
这个性质的意思就是说不同的高斯核对图像的平滑是连续的。
3)局部极值递性
这个特征可以从人眼的视觉原理去理解,人在看一件物体时,离得越远,物体的细节看到的越少,细节特征是在减少的。高斯核对图像进行滤波具有压制局部细节的性质。
4)尺度伸缩不变性。
这里只是一个公式推导的问题,对原来的信号加一个变换函数,对变换后的信号再进行高斯核的尺度空间生成,新的信号的极值点等特征是不变的。
参考图像的矩特征
图像识别的一个核心问题是图像的特征提取,简单描述即为用一组简单的数据(图像描述量)来描述整个图像,这组数据越简单越有代表性越好。良好的特征不受光线、噪点、几何形变的干扰。图像识别发展几十年,不断有新的特征提出,而图像不变矩就是其中一个。
矩是概率与统计中的一个概念,是随机变量的一种数字特征。设X为随机变量,c为常数,k为正整数。则量\(E[(x-c)^k]\)称为X关于c点的k阶矩。
比较重要的有两种情况:
c=0。这时\(a_k=E(X^k)\)称为X的k阶原点矩
\(c=E(X)\)。这时\(\mu_k=E[(X-EX)^k]\)称为X的k阶中心矩。
一阶原点矩就是期望。一阶中心矩\(\mu_1=0\),二阶中心矩\(\mu_2\)就是X的方差\(Var(X)\)。在统计学上,高于4阶的矩极少使用。\(\mu_3\)可以去衡量分布是否有偏。\(\mu_4\)可以去衡量分布(密度)在均值附近的陡峭程度如何。
针对于一幅图像,我们把像素的坐标看成是一个二维随机变量(X,Y),那么一幅灰度图像可以用二维灰度密度函数来表示,因此可以用矩来描述灰度图像的特征。
不变矩(Invariant Moments)是一处高度浓缩的图像特征,具有平移、灰度、尺度、旋转不变性。M.K.Hu在1961年首先提出了不变矩的概念。1979年M.R.Teague根据正交多项式理论提出了Zernike矩。下面主要介绍这两种矩特征的算法原理与实现。
一幅M×N的数字图像\(f(i,j)\),其p+q阶几何矩\(m_pq\)和中心矩\(\mu_{pq}\)为:
\[ m_{pq}=\sum_{i=1}^M\sum_{j=1}^Ni^pj^qf(i,j) \\ \mu_{pq}=\sum_{i=1}^M\sum_{j=1}^N(i-\bar{i})^p(j-\bar{j})^qf(i,j) \]
其中\(f(i,j)\)为图像在坐标点(i,j)处的灰度值。\(\bar{i}=\frac{m_{10}}{m_{00}},\bar{j}=\frac{m_{01}}{m_{00}}\)
若将\(m_{00}\)看作是图像的灰度质量,则\((\bar{i},\bar{j})\)为图像的质心坐标,那么中心矩\(\mu_{pq}\)反映的是图像灰度相对于其灰度质心的分布情况。可以用几何矩来表示中心矩,0~3阶中心矩与几何矩的关系如下:
下图中\(\bar{x}=\bar{i},\bar{y}=\bar{j}\)
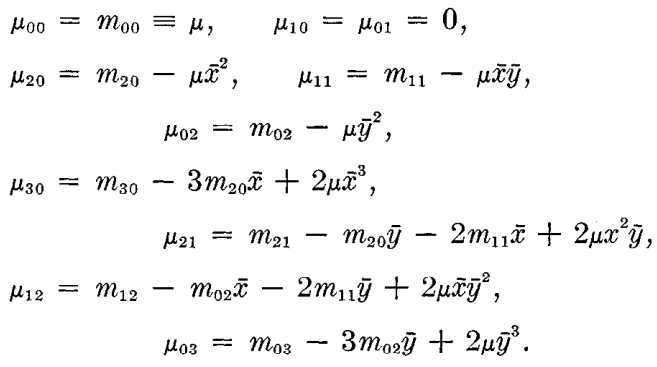
为了消除图像比例变化带来的影响,定义规格化中心矩如下:
\[ \eta_{pq}=\frac{\mu_{pq}}{\mu_{00}^\gamma},(\gamma=1+\frac{p+q}{2},p+q \geqslant 2) \]
利用二阶和三阶规格中心矩可以导出下面7个不变矩组\((\Phi_1~\Phi_7)\),它们在图像平移、旋转和比例变化时保持不变:
\[ \begin{array}{l} \Phi_1= \eta _{20}+ \eta _{02} \\ \Phi_2=( \eta _{20}- \eta _{02})^{2}+4 \eta _{11}^{2} \\ \Phi_3=( \eta _{30}-3 \eta _{12})^{2}+ (3 \eta _{21}- \eta _{03})^{2} \\ \Phi_4=( \eta _{30}+ \eta _{12})^{2}+ ( \eta _{21}+ \eta _{03})^{2} \\ \Phi_5=( \eta _{30}-3 \eta _{12})( \eta _{30}+ \eta _{12})[( \eta _{30}+ \eta _{12})^{2}-3( \eta _{21}+ \eta _{03})^{2}]+(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \Phi_6 =( \eta _{20}- \eta _{02})[( \eta _{30}+ \eta _{12})^{2}- ( \eta _{21}+ \eta _{03})^{2}]+4 \eta _{11}( \eta _{30}+ \eta _{12})( \eta _{21}+ \eta _{03}) \\ \Phi_7=(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}]-( \eta _{30}-3 \eta _{12})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \end{array}\]
使用opencv可以方便的计算:
int main(int argc, char** argv)
{
Mat image = imread(argv[1]);
cvtColor(image, image, CV_BGR2GRAY);
Moments mts = moments(image);
double hu[7];
HuMoments(mts, hu);
for (int i=0; i<7; i++)
{
cout << log(abs(hu[i])) <<endl;
}
return 0;
}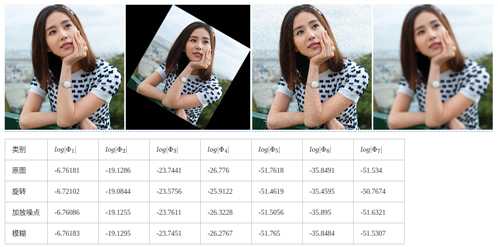
可以看到图像虽然发生了各种变化,但是矩的值基本保持不变。
参考Harris角点
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内就不存在角点;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
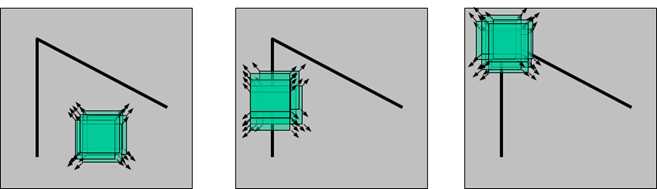
对于图像\(I(x,y)\),当在点\((x,y)\)处平移\((\Delta x,\Delta y)\)后的自相似性,可以通过自相关函数给出:
\[c(x,y;\Delta x,\Delta y) = \sum_{(u,v)\in W(x,y)}w(u,v)(I(u,v) – I(u+\Delta x,v+\Delta y))^2\]
其中,\(W(x,y)\)是以点(x,y)为中心的窗口,\(w(u,v)\)为加权函数,它既可是常数,也可以是高斯加权函数。

根据泰勒展开,对图像\(I(x,y)\)在平移\((\Delta x,\Delta y)\)后进行一阶近似:
\[I(u+\Delta x,v+\Delta y) = I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y+O(\Delta x^2,\Delta y^2)\approx I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y\]
其中,\(I_x,I_y\)是图像\(I(x,y)\)的偏导数,这样的话,自相关函数则可以简化为:
\[c(x,y;\Delta x,\Delta y)\approx \sum_w (I_x(u,v)\Delta x+I_y(u,v)\Delta y)^2=[\Delta x,\Delta y]M(x,y)\begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix}\]
其中
\[M(x,y)=\sum_w \begin{bmatrix}I_x(x,y)^2&I_x(x,y)I_y(x,y) \\ I_x(x,y)I_y(x,y)&I_y(x,y)^2\end{bmatrix} = \begin{bmatrix}\sum_w I_x(x,y)^2&\sum_w I_x(x,y)I_y(x,y) \\\sum_w I_x(x,y)I_y(x,y)&\sum_w I_y(x,y)^2\end{bmatrix}=\begin{bmatrix}A&C\\C&B\end{bmatrix}\]
也就是说图像\(I(x,y)\)在点(x,y)处平移\((\Delta x,\Delta y)\)后的自相关函数可以近似为二项函数:
\[c(x,y;\Delta x,\Delta y)\approx A\Delta x^2+2C\Delta x\Delta y+B\Delta y^2\]
其中
\[A=\sum_w I_x^2, B=\sum_w I_y^2,C=\sum_w I_x I_y\]
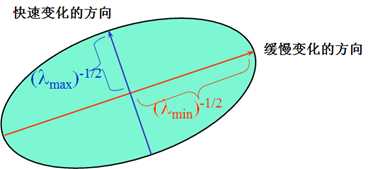
二次项函数本质上就是一个椭圆函数。椭圆的扁率和尺寸是由\(M(x,y)\)的特征值\(\lambda_1、\lambda_2\)决定的,椭圆的方向是由\(M(x,y)\)的特征矢量决定的,如下图所示,椭圆方程为:
\[[\Delta x,\Delta y]M(x,y)\begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix} = 1\]
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
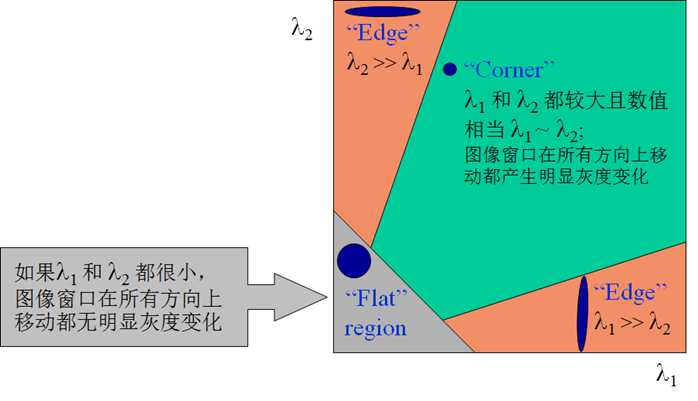
根据二次项函数特征值的计算公式,我们可以求M(x,y)矩阵的特征值。但是Harris给出的角点差别方法并不需要计算具体的特征值,而是计算一个角点响应值R来判断角点。R的计算公式为:
\[R=det \boldsymbol{M} - \alpha(trace\boldsymbol{M})^2\]
式中,\(det \boldsymbol{M}\)为矩阵\(\boldsymbol{M}=\begin{bmatrix}A&B\\B&C\end{bmatrix}\)的行列式;\(trace\boldsymbol{M}\)为矩阵M的直迹;\(\alpha\)为经常常数,取值范围为0.04~0.06。事实上,特征是隐含在\(det \boldsymbol{M}\)和\(det \boldsymbol{M}\)中,因为,
\[det\boldsymbol{M} = \lambda_1\lambda_2=AC-B^2 \\ trace\boldsymbol{M}=\lambda_2+\lambda_2=A+C\]
Harris角点检测算子对亮度和对比度的变化不敏感;
这是因为在进行Harris角点检测时,使用了微分算子对图像进行微分运算,而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之,对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置,但是,由于阈值的选择,可能会影响角点检测的数量。
Harris角点检测算子具有旋转不变性
Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆,椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时,特征值并不发生变化,所以判断角点响应值R也不发生变化,由此说明Harris角点检测算子具有旋转不变性。
Harris角点检测算子不具有尺度不变性
Features from Accelerated Segment Test
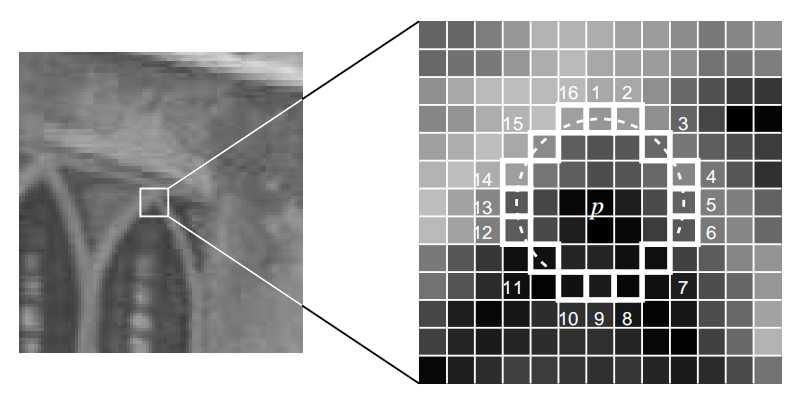
从邻近的位置选取了多个特征点是另一个问题,我们可以使用Non-Maximal Suppression来解决。
Binary Robust Independent Elementary Features
参考BRIEF 特征描述子
BRIEF提供了一种计算二值串的捷径,而并不需要去计算一个类似于SIFT的特征描述子。它需要先平滑图像,然后在特征点周围选择一个Patch,在这个Patch内通过一种选定的方法来挑选出来\(n_d\)个点对。然后对于每一个点对\((p,q)\),我们来比较这两个点的亮度值,如果\(I(p)>I(q)\)则这个点对生成了二值串中一个的值为1,如果\(I(p)<I(q)\),则对应在二值串中的值为-1,否则为0。所有\(n_d\)个点对,都进行比较之间,我们就生成了一个\(n_d\)长的二进制串。
设我们在特征点的邻域块大小为\(S*S\)内选择\(n_d\)个点对\((p,q)\),实验中测试了5种采样方法:
1)在图像块内平均采样;
2)p和q都符合\((0,\frac{1}{25}S^2)\)的高斯分布;
3)p符合\((0,\frac{1}{25}S^2)\)的高斯分布,而q符合\((0,\frac{1}{100}S^2)\)的高斯分布;
4)在空间量化极坐标下的离散位置随机采样
5)把p固定为(0,0),q在周围平均采样

第二种效果比较好;
Oriented FAST and Rotated BRIEF
参考ORB特征点检测
ORB特征是将FAST特征点的检测方法与BRIEF特征描述子结合起来,并在它们原来的基础上做了改进与优化。
我们知道FAST特征点是没有尺度不变性的,所以我们可以通过构建高斯金字塔,然后在每一层金字塔图像上检测角点,来实现尺度不变性。那么,对于局部不变性,我们还差一个问题没有解决,就是FAST特征点不具有方向,ORB的论文中提出了一种利用灰度质心法来解决这个问题,灰度质心法假设角点的灰度与质心之间存在一个偏移,这个向量可以用于表示一个方向。对于任意一个特征点p来说,我们定义p的邻域像素的矩为:
\[m_{pq} = \sum_{x,y}x^py^qI(x,y)\]
其中\(I(x,y)\)为点(x,y)处的灰度值。那么我们可以得到图像的质心为:
\[C = \left(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}}\right)\]
那么特征点与质心的夹角定义为FAST特征点的方向:
\[\theta = arctan(m_{01},m_{10})\]
为了提高方法的旋转不变性,需要确保x和y在半径为r的圆形区域内,即\(x,y\in [-r,r]\),r等于邻域半径。
ORB选择了BRIEF作为特征描述方法,但是我们知道BRIEF是没有旋转不变性的,所以我们需要给BRIEF加上旋转不变性,把这种方法称为“Steer BREIF”。对于任何一个特征点来说,它的BRIEF描述子是一个长度为n的二值码串,这个二值串是由特征点周围n个点对(2n个点)生成的,现在我们将这2n个点\((x_i,y_i),i=1,2,?,2n\)组成一个矩阵S
\[S =\begin{pmatrix}x_1&x_2&\cdots&x_{2n}\\y_1&y_2&\cdots&y_{2n}\end{pmatrix}\]
Calonder建议为每个块的旋转和投影集合分别计算BRIEF描述子,但代价昂贵。ORB中采用了一个更有效的方法:使用邻域方向θ和对应的旋转矩阵\(R_θ\),构建S的一个校正版本\(S_θ\)
\[S_{\theta} = R_{\theta}S\]
其中:
\[R_{\theta} = \begin{bmatrix}cos\theta & sin\theta \\ –sin\theta &cos\theta\end{bmatrix}\]
实际上,我们可以把角度离散化,即把360度分为12份,每一份是30度,然后我们对这个12个角度分别求得一个Sθ,这样我们就创建了一个查找表,对于每一个θ,我们只需查表即可快速得到它的点对的集合\(S_θ\)。
BRIEF令人惊喜的特性之一是:对于n维的二值串的每个比特征位,所有特征点在该位上的值都满足一个均值接近于0.5,而方差很大的高斯分布。方差越大,说明区分性越强,那么不同特征点的描述子就表现出来越大差异性,对匹配来说不容易误配。但是当我们把BRIEF沿着特征点的方向调整为Steered BRIEF时,均值就漂移到一个更加分散式的模式。可以理解为有方向性的角点关键点对二值串则展现了一个更加均衡的表现。而且论文中提到经过PCA对各个特征向量进行分析,得知Steered BRIEF的方差很小,判别性小,各个成分之间相关性较大。
为了减少Steered BRIEF方差的亏损,并减少二进制码串之间的相关性,ORB使用了一种学习的方法来选择一个较小的点对集合。方法如下:
首先建立一个大约300k关键点的测试集,这些关键点来自于PASCAL2006集中的图像。
对于这300k个关键点中的每一个特征点,考虑它的31×31的邻域,我们将在这个邻域内找一些点对。不同于BRIEF中要先对这个Patch内的点做平滑,再用以Patch中心为原点的高斯分布选择点对的方法。ORB为了去除某些噪声点的干扰,选择了一个5×5大小的区域的平均灰度来代替原来一个单点的灰度,这里5×5区域内图像平均灰度的计算可以用积分图的方法。我们知道31×31的Patch里共有N=(31?5+1)×(31?5+1)个这种子窗口,那么我们要N个子窗口中选择2个子窗口的话,共有\(C^2_N\)种方法。所以,对于300k中的每一个特征点,我们都可以从它的31×31大小的邻域中提取出一个很长的二进制串,长度为\(M = C_N^2\),表示为
\[binArray = [p_1,p_2,\cdots,p_M],p_i\in\{0,1\}\]
那么当300k个关键点全部进行上面的提取之后,我们就得到了一个300k×M的矩阵,矩阵中的每个元素值为0或1。
进行贪婪搜索:从T中把排在第一的那个列放到R中,T中就没有这个点对了测试结果了。然后把T中的排下一个的列与R中的所有元素比较,计算它们的相关性,如果相关超过了某一事先设定好的阈值,就扔了它,否则就把它放到R里面。重复上面的步骤,只到R中有256个列向量为止。如果把T全找完也,也没有找到256个,那么,可以把相关的阈值调高一些,再重试一遍。这样,我们就得到了256个点对。上面这个过程我们称它为rBRIEF。
结合test/openvslam/feature/orb_extractor.cc代码,逐步分析特征提取过程。openvslam提取的特征的一个显著特征就是十分均匀,下文会详细分析实现的方法。
首先定义orb参数
const auto params = feature::orb_params();
// -- src/openvslam/feature/orb_params.h
// 最多关键点的个数
unsigned int max_num_keypts_ = 2000;
// 图像金字塔缩放比例
float scale_factor_ = 1.2;
// 图像金字塔层数
unsigned int num_levels_ = 8;
// FAST脚点检测的灰度差门限
unsigned int ini_fast_thr_ = 20;
// 如果上面的门限没有检测到角点,改用更小的门限值
unsigned int min_fast_thr = 7;然后定义特征提取器
auto extractor = feature::orb_extractor(params);此时做一些初始化
计算图像金塔每一层的缩放系数(以及倒数)、系数的平方(以及倒数);
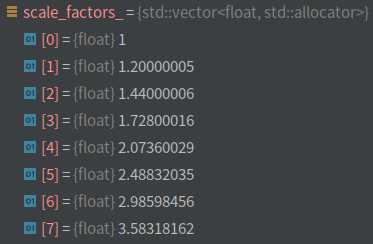
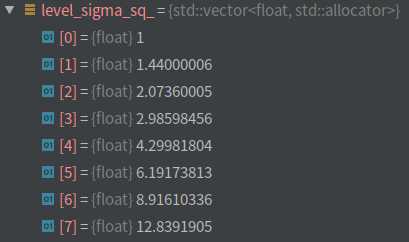
根据设定的最大特征点数目计算图像金字塔中每层对应的特征点数;
\[N*\frac{1-a}{1-a^n} + N*\frac{1-a}{1-a^n}*a + \cdots+ N*\frac{1-a}{1-a^n}*a^{n-1}\approx N \\
a=\frac{1}{scale},N=最大特征点数,n=金字塔层数\]
这里层与层之间的特征点数满足缩放因子,但是实际上应该满足平方的关系,但是这样的数列不好找。
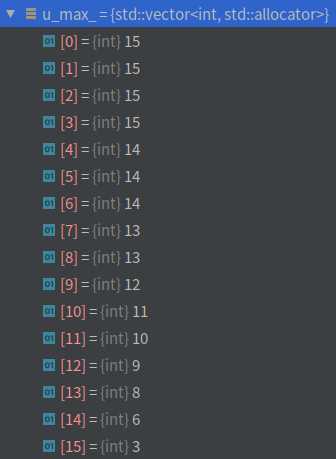
std::vector<cv::KeyPoint> keypts;
cv::Mat desc;
extractor.extract(img, mask, keypts, desc);//直接resize
cv::resize(image_pyramid_.at(level - 1), image_pyramid_.at(level), size, 0, 0, cv::INTER_LINEAR);用户可以自定义任意个数的矩形mask区域,不进行特征点提取;也可以使用更细致的image mask;
//[x_min / cols, x_max / cols, y_min / rows, y_max / rows]
std::vector<std::vector<float>> mask_rects_;
void orb_extractor::create_rectangle_mask(const unsigned int cols, const unsigned int rows) {
// rect_mask_和原图有同样的尺寸,初始填充数值为255
if (rect_mask_.empty()) {
rect_mask_ = cv::Mat(rows, cols, CV_8UC1, cv::Scalar(255));
}
// 根据mask_rects_得到mask区域
for (const auto& mask_rect : orb_params_.mask_rects_) {
// draw black rectangle
const unsigned int x_min = std::round(cols * mask_rect.at(0));
const unsigned int x_max = std::round(cols * mask_rect.at(1));
const unsigned int y_min = std::round(rows * mask_rect.at(2));
const unsigned int y_max = std::round(rows * mask_rect.at(3));
// 将mask区域数值改为0
cv::rectangle(rect_mask_, cv::Point2i(x_min, y_min), cv::Point2i(x_max, y_max), cv::Scalar(0), -1, cv::LINE_AA);
}
}
//BRIEF orientation
static constexpr unsigned int fast_patch_size_ = 31;
//half size of FAST patch
static constexpr int fast_half_patch_size_ = fast_patch_size_ / 2;
//size of maximum ORB patch radius
static constexpr unsigned int orb_patch_radius_ = 19;
// 珊格化有效图像区域
constexpr unsigned int cell_size = 64;
// 珊格化之后每个珊格与相邻的珊格有一定的重叠区域
constexpr unsigned int overlap = 6;程序流程:
遍历图像金字塔每一层
根据orb_patch_radius_计算出该层的边界,从而确定该层有效搜索区域的HxW
按照cell_size对该有效区域珊格化,珊格中有任何在mask内,则不对该珊格进行特征点计算,剔除该珊格
对珊格进行FAST检测,首先使用较大的门限ini_fast_thr_,如果没有检测到FAST关键点,再使用较小的门限min_fast_thr进行检测
将检测到的特征点确认不再mask中后添加到该层特征点集合中
通过树形结构筛选该层的特征点
调整使用cv::FAST计算的特征点中的patch直径,原始是7,设置为31(rBRIEF描述子的patch size)* scale_factor(金字塔层数的比例因子) 以及 _octave值
计算FAST特征点的方向,和论文中一致,计算图像的矩
通过树形结构筛选特征点
初始化根结点
迭代展开其子节点
一个父节点对应展开4个子叶节点 将一个矩形等分为4等份,每份为被一个子叶节点掌握,将父节点中的特征点分配代各自的子叶节点中
展开的叶节点数 >= 该层的目标特征点数 或者 叶节点数不再发生变化则跳出迭代
在将每个节点中响应值最大(特征最好)的特征点当作该节点上的特征点
由于每个子叶节点均是由上层等分展开的,所得到的特征点在图像平面上分布就十分均匀
/*
_pt: 关键点的像素坐标(x,y)
_size: 关键点patch直径,像素点
_angle: 关键点的方向
_response: 响应值,越大越好
_octave: 关键点位于图像金字塔的层数
_class_id: 关键点的类别ID
*/
KeyPoint(Point2f _pt, float _size, float _angle=-1, float _response=0, int _octave=0, int _class_id=-1);
const unsigned int num_initial_nodes = std::round(static_cast<double>(max_x - min_x) / (max_y - min_y));
// 节点的结构
class orb_extractor_node {
public:
orb_extractor_node() = default;
// 一个父节点对应展开4个子叶节点 将一个矩形等分为4等份,每份为被一个子叶节点掌握
std::array<orb_extractor_node, 4> divide_node();
// 以该结点为父节点的特征点
std::vector<cv::KeyPoint> keypts_;
// 该节点掌控的区域,矩形的对角点
cv::Point2i pt_begin_, pt_end_;
std::list<orb_extractor_node>::iterator iter_;
bool is_leaf_node_ = false;
};
// nodes是链表结构,为了方便给指定的node中添加特征点,使用vector保存每个node的指针
std::list<orb_extractor_node> nodes;
std::vector<orb_extractor_node*> initial_nodes;
// 用于判断(x,y)是否为mash点
auto is_in_mask = [&mask](const unsigned int y, const unsigned int x, const float scale_factor) {
return mask.at<unsigned char>(y * scale_factor, x * scale_factor) == 0;
};
#pragma omp critical [(name)] //[]表示名字可选
{
...
}和论文中一致,作者借鉴opencv中实现的方法。
计算描述子
图像进行高斯平滑
计算描述子以及方向,每个关键点生成一个32字节的描述子将所有图像金字塔中的特征点位置统一到原始图像中的相应的位置;
标签:正交 简化 规格 高斯金字塔 不容易 关键点 优化 取出 node
原文地址:https://www.cnblogs.com/hardjet/p/11438707.html