标签:text 输入数据 transform 存在 计算 mic 节点 display 输出矩阵
???????传统CNN卷积可以处理图片等欧式结构的数据,却很难处理社交网络、信息网络等非欧式结构的数据。一般图片是由c个通道h行w列的矩阵组成的,结构非常规整。而社交网络、信息网络等是图论中的图(定点和边建立起的拓扑图)。
???????传统CNN卷积面对输入数据维度必须是确定的,进而CNN卷积处理后得到的输出数据的维度也是确定的。欧式结构数据中的每个点周边结构都一样,如一个像素点周围一定有8个像素点,即每个节点的输入维度和输出维度都是固定的。而非欧式结构数据则不一定,如社交网络中A和B是朋友,A有n个朋友,但B不一定有n个朋友,即每个节点的输入维度和输出维度都是不确定的。
???????所以不能使用CNN来对社交网络、信息网络等数据进行处理,因为对A节点处理后得到输出数据的维度和对B节点处理后得到输出数据维度是不一样的。为了得到社交网络、信息网络的空间特征所以我们使用GCN(Graph Convolutional Network)来处理。
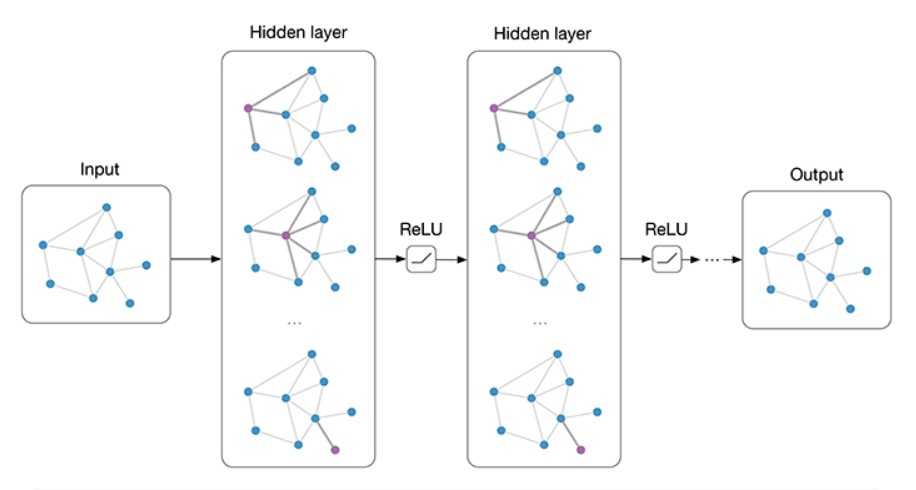
???????同一般的卷积神经网络不同,GCN输入的数据是一个图拓扑矩阵,这个拓扑矩阵一般是图的邻接矩阵。
| 概念 | 定义 |
|---|---|
| G | 一个拓扑图定义为G=(V,E) 其中V是节点集合,E是边集合。 |
| N | N是图中节点个数,即|V| |
| F | 节点的特征数,不同学习任务F不同 |
| X | 网络初始化矩阵, X是N行F列的矩阵 |
| D | 图的度矩阵,Dij表示点i和点j是否存在连接 |
| A | 图结构表征矩阵, A是N行N列的矩阵,A通常是G的邻接矩阵 |
| Hi | GCN中每层输出矩阵 Hi是一个N行F列矩阵 |
| Wi | GCN中每层权值矩阵 Wi是一个F行F列矩阵 |
???????在GCN中,第1层又H0 = X,从i层到i+1层网络计算其中一个简单传播规则,即传播规则1:
\[\begin{array}{l} {{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\ \quad \;\;\; = \sigma \left( {{\bf{A}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\ \end{array}\]
???????其中激活函数σ一般为ReLu函数。尽然这个规则下GCN是一个简单模型,但已经足够强大,当然实际使用传播规则是下面几个:
???????传播规则2
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {{{\bf{D}}^{ - \frac{1}{2}}}{\bf{A}}{{\bf{D}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
???????传播规则3
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {\left( {{\bf{I}} + {{\bf{D}}^{ - \frac{1}{2}}}{\bf{A}}{{\bf{D}}^{ - \frac{1}{2}}}} \right){{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
???????传播规则4
\[\begin{array}{l} {{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\ \quad \;\;\; = \sigma \left( {{{\bf{D}}^{ - \frac{1}{2}}}\left( {{\bf{D}} - {\bf{A}}} \right){{\bf{D}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\ \end{array}\]
???????传播规则5
\[\begin{array}{l}
{{\bf{H}}^{i + 1}} = f\left( {{{\bf{H}}^i},{\bf{A}}} \right) \\
\quad \;\;\; = \sigma \left( {{{{\bf{\hat D}}}^{ - \frac{1}{2}}}{\bf{\hat A}}{{{\bf{\hat D}}}^{ - \frac{1}{2}}}{{\bf{H}}^i}{{\bf{W}}^i}} \right) \\
\end{array}\]
???????其中\({\bf{\hat A}}{\rm{ = }}{\bf{A}}{\rm{ + }}{\rm I}\),I是一个N×N的单位矩阵。而\({\bf{\hat D}}\)是\({\bf{\hat A}}\)
是一个对角线矩阵,其中${{\bf{\hat D}}{ii}} = \sum\limits_j {{{{\bf{\hat A}}}{ij}}} $。
???????最后根据不同深度学习任务来定制相应的GCN网络输出。
???????文本分类是自然语言处理比较常见的问题,常见的文本分类主要基于传统的cnn、lstm以及最近几年比较热门的transform、bert等方法,传统分类的模型主要处理排列整齐的矩阵特征,也就是很多论文中提到的Euclidean Structure,但是我们科学研究或者工业界的实际应用场景中,往往会遇到非Euclidean Structure的数据,如社交网络、信息网络,传统的模型无法处理该类数据,提取特征进一步学习,因此GCN 应运而生,本文主要介绍GCN在文本分类中的应用。
???????首先我们将我们的文本语料构建拓扑图,改图的节点由文档和词汇组成,即图中节点数|v|=|doc|+|voc| 其中|doc|表示文档数,|voc|表示词汇总量,对于特征矩阵X,我们采用单位矩阵I表示,即每个节点的向量都是one-hot形式表示,下面我们将介绍如何定义邻接矩阵A,其公式如所示,对于文档节点和词汇节点的权重,我们采用TF-IDF表示,对于词汇节点之间的权重,我们采用互信息表示(PMI, point-wise mutual information),在实验中,PMI表现好于两个词汇的共现词汇数,其公式如所示:
\[{A_{ij}} = \left\{ \begin{array}{l}
{\rm{PMI}}\left( {i,j} \right)\quad \quad \quad \quad i和j是词语而且{\rm{PMI}}\left( {i,j} \right) > {\rm{0}} \\
{\rm{TF - IDF}}\left( {i,j} \right)\quad \;\;i是文档j是词语 \\
1\quad \quad \quad \quad \quad \quad \quad \;\;\;i = j \\
0\quad \quad \quad \quad \quad \quad \quad \;\;其他\\
\end{array} \right.\]
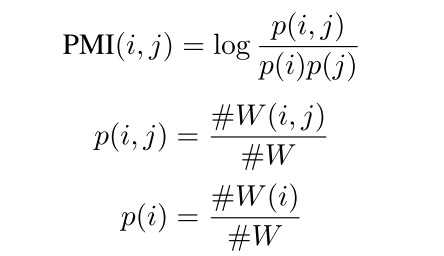
???????其中#W(i)表示在固定滑动窗口下词汇i出现的数量,#W(i, j)表示在固定滑动窗口下词汇i,j同时出现的数量,当PMI(i, j)为正数表示词汇i和词汇j有较强的语义关联性,当PMI(i, j)为负数的时候表示词汇i,j语义关联性较低,在构建完图后,我们代入GCN中,构建两层GCN,如下:
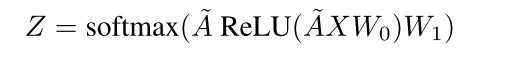
???????我们采用经典的交叉熵来定义损失函数:
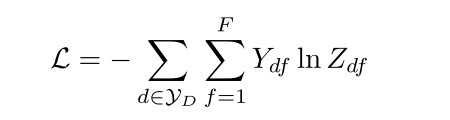
???????其中YD表示带标签的文挡集合,Ydf 表示标注类别,Zdf为预测的类别。
???????下面介绍GCN在多个公开数据集上的实验结果,其中数据源为:

???????GCN在文本分类上的实验结果见表2。
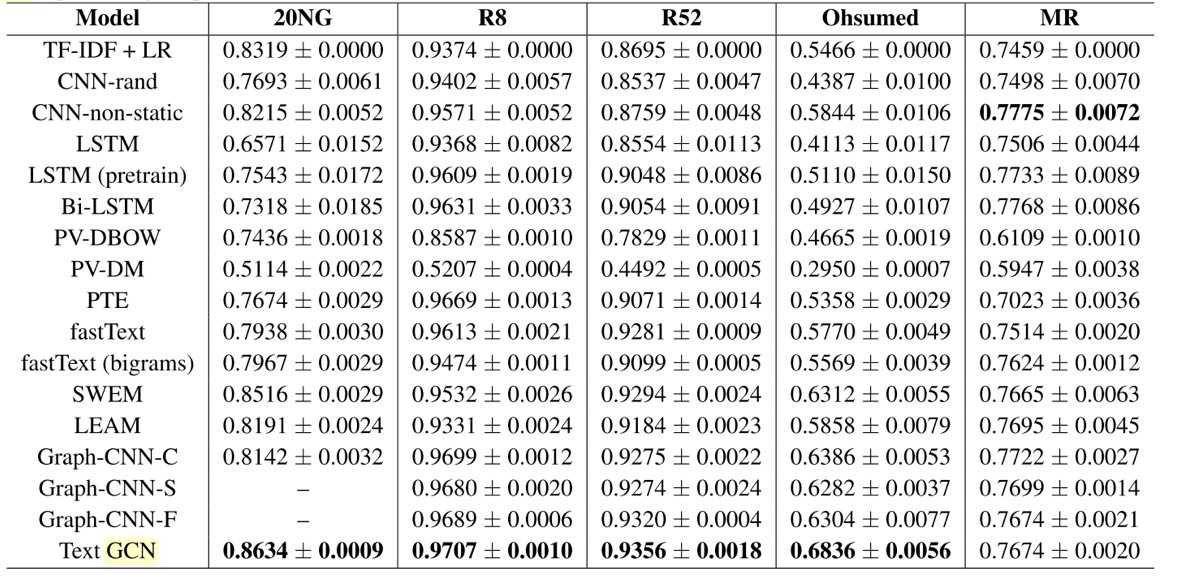
???????这种新颖的文本分类方法称为文本图卷积网络(Text-GCN),巧妙地将文档分类问题转为图节点分类问题。Text-GCN可以很好地捕捉文档地全局单词共现信息和利用好文档有限地标签。一个简单的双层Text-GCN已经取得良好地成果。
[1] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
[2] Yao L, Mao C, Luo Y. Graph convolutional networks for text classification[J]. arXiv preprint arXiv:1809.05679, 2018.
[3] http://tkipf.github.io/graph-convolutional-networks/
标签:text 输入数据 transform 存在 计算 mic 节点 display 输出矩阵
原文地址:https://www.cnblogs.com/Kalafinaian/p/11440732.html