标签:time 逆序数 pre == flag ack 条件 http 今天
正好今天学习OI一整年,发篇博客纪念纪念。
听说联赛现在全国排名?那完了,一年OI一场空。
记得去年这个时候刚学OI,跟那些初中就开始学的大佬听课,第一节他们就讲2-sat,第二节就是线性代数。
我的内心是


然后,我就自闭了一个月。
如今又来看这些玄学玩意儿。
先列一下知识点(显得我更像是抄课件了呢)
线性基
高斯消元
行列式(主要是矩阵树定理)
矩阵的幂(邻接矩阵、矩阵加速递推)
(以后可能会写总结吧,咕,我在)
还记得上一个专场是什么吗?
打表找规律,乱搞出奇迹,我对拍了17分钟你能秒我?
我们又来看一道博弈(×)找规律(√)的题目
依然是n堆石子
第一个回合,先手可以直接拿走若干个整堆的石子。可以一堆都不拿,但不可以全部拿走。
第二回合也一样,后手也有这样一次机会。
从第三个回合开始(又轮到先手)的规则和nim游戏一样。
问先手是否有必胜策略,如果有,还要让先手拿走的石子总数尽量小。
我们想一想nim游戏是先手必败的情形是什么?
一般nim游戏的必败条件是所有数异或为0。
所以,我们无论如何也不能让后拿的人有这个机会
而如果先拿的人剩下的石子堆中存在一些石子堆的数目异或起来为0,也就是它的某个子集满足nim游戏的必败条件
那么第二个人只需要把其它的石子堆拿走第一个人就必败,反之第一个人必胜。
所以我们必须保证第一个人剩下的石子堆的任意子集异或起来不为0
在线性代数中,我们称剩下的数在二进制位上线性无关
题目也就转化成了从n个数中选一些数,使得它们在二进制位上线性无关,且和最大
这题就是求和最大的线性基,只需要排序一下再选就好了,有点像最小生成树
推荐一个线性基的博客
注意开longlong
代码
#include<cstdio>
#include<algorithm>
using namespace std;
int n,vis[105],a[105],b[55];long long ans;
bool insert(int val)
{
for(int i=30;i>=0;i--)
if(val&(1<<i))
{
if(!b[i]){b[i]=val;break;}
val^=b[i];
}
return val>0;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
sort(a+1,a+1+n);
for(int i=n;i>=1;i--)vis[i]=insert(a[i]);
for(int i=1;i<=n;i++)ans+=vis[i]?0:a[i];
printf("%lld\n",ans);
}
给定一些数,求这些数通过异或能得到的数中的第k小是多少。
好像是线性基的板题。线性基能组合出来的数的个数是2^(向量个数),把k做二进制拆分就好了
代码
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
vector<int>g;int T,n,m,q;long long a,A[105];
void insert(long long a)
{
for(int i=60;i>=0&&a;i--)
{
if(!((1ll<<i&a)))continue;
if(A[i]){a^=A[i];continue;}
for(int j=0;j<i;j++)if(a&(1ll<<j))a^=A[j];
for(int j=i+1;j<=60;j++)if(A[j]&(1ll<<i))A[j]^=a;
A[i]=a;break;
}
}
int main()
{
scanf("%d",&T);
for(int it=1;it<=T;it++)
{
memset(A,0,sizeof A);g.clear();m=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld",&a),insert(a);
for(int i=0;i<=60;i++)if(A[i])g.push_back(A[i]),m++;
printf("Case #%d:\n",it);scanf("%d",&q);
for(int i=1;i<=q;i++)
{
long long k;scanf("%lld",&k);
k-=(m!=n);
if((1ll<<m)-1ll<k)printf("-1\n");
else
{
long long ans=0;
for(int i=0;i<m;i++)if((1ll<<i)&k)ans^=g[i];
printf("%lld\n",ans);
}
}
}
}
n个点,m条边的连通无向图,边的权值从1到n
一开始在1号点,每次等概率走向当前点的邻接点
问怎样给边赋权值,使得走到n号点时期望走过的边权和最小
走到n号点时期望走过的边权和=每条边 期望走过次数*边权 的和
边(u,v)期望走过次数=点u期望走过次数/u的度数+点v期望走过次数/v的度数
即E((u,v))=E(u)/deg(u)+E(v)/deg(v)
设v是u的邻接点,再考虑E(u)和E(v)之间的关系
E(1)=1+sum_v E(v)/deg(v) (v!=n,v是1的邻接点)
E(u)=sum_v E(v)/deg(v) (1<u<n,v!=n,v是u的邻接点)
E(n)=0
n-1个方程,n-1个未知数,高斯消元一发
最后贪心
按照边走过的期望次数赋权值
边走过的期望次数越少,就赋越大的权值
代码
#include<cstdio>
#include<cstring>
#define maxn 505
#include<algorithm>
using namespace std;
int n,m,deg[maxn],lin[maxn*maxn][2];
double eq[maxn][maxn],E[maxn],El[maxn*maxn];
bool no(double x){return -1e-10<x&&x<1e-10;}
void Gauss()
{
for(int i=1;i<=n;i++)
{
if(no(eq[i][i])){for(int j=i+1;j<=n;j++)if(!no(eq[j][i])){swap(eq[i],eq[j]);break;}}
for(int j=1;j<=n;j++)if(j!=i&&!no(eq[j][i]))
{
double t=eq[j][i]/eq[i][i];
for(int k=1;k<=n+1;k++)eq[j][k]=eq[j][k]-eq[i][k]*t;
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d",&lin[i][0],&lin[i][1]),deg[lin[i][0]]++,deg[lin[i][1]]++;
eq[n][n]=1.000;eq[1][n+1]=-1.0;
for(int i=1;i<n;i++)eq[i][i]=-1.0;
for(int i=1;i<=m;i++)if(lin[i][0]!=n&&lin[i][1]!=n)
eq[lin[i][0]][lin[i][1]]=1.0/double(deg[lin[i][1]]),eq[lin[i][1]][lin[i][0]]=1.0/double(deg[lin[i][0]]);
Gauss();
for(int i=1;i<=n;i++)E[i]=eq[i][n+1]/eq[i][i];
for(int i=1;i<=m;i++)El[i]=E[lin[i][0]]/double(deg[lin[i][0]])+E[lin[i][1]]/double(deg[lin[i][1]]);
sort(El+1,El+1+m);
double ans=0;
for(int i=1;i<=m;i++)ans+=El[i]*double(m-i+1);
printf("%.3lf\n",ans);return 0;
}
保证源点和汇点数目相同。
考虑所有把源汇点两两配对,并用两两不相交的路径把它们两两连接起来的所有方案。
如果这个方案中,把源点按标号1到n排序后,得到的对应汇点序列的逆序数对的个数是奇数,那么A给B一块钱,否则B给A一块钱。
问最后A的收益,对大质数取模。
n ≤ 600
先不考虑不相交路径的限制
令f[i][j]为从第i个无入度的点走到第j个无出度的点的方案数
由行列式的定义,这个矩阵的行列式的值就是答案(每一项前的正负由逆序对个数的奇偶性决定)
再考虑路径不相交的情形,发现答案不变
这是因为对于任一种两条路径相交的方案x,选择这对路径上相交的最后一个点,将这个点之后的路径反转,一定会映射到另一种路径相交的方案y
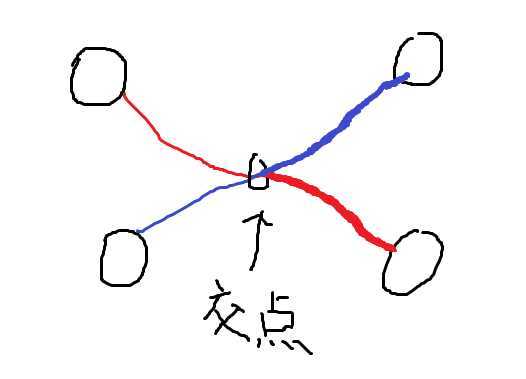
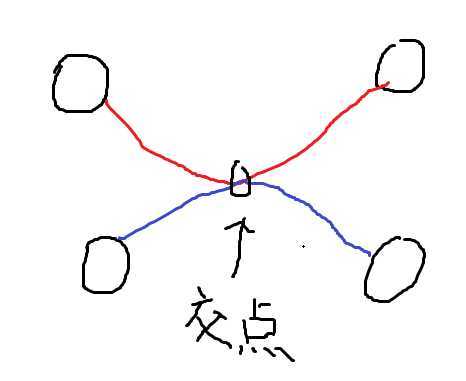
且方案y对答案的贡献刚好和x对答案的贡献相反(逆序数奇偶发生改变)
f[i][j]可以用拓补序来dp转移(好像是我第一次写)
代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=605,maxm=100005;
int n,m,cnt,be,en,en1,en2,ans,mod,flag,S[maxn],T[maxn],f[maxn][maxn];
int v[maxm],in[maxn],nex[maxm],out[maxn],top[maxn],info[maxn],eq[maxn][maxn];
void add(int u,int v1){nex[++cnt]=info[u];info[u]=cnt;v[cnt]=v1;}
int qp(int a,int k){int res=1;while(k){if(k&1)res=1ll*res*a%mod;k>>=1;a=1ll*a*a%mod;}return res;}
void Gauss()
{
for(int i=1;i<=en1;i++)
{
if(!eq[i][i]){for(int j=i+1;j<=en1;j++)if(eq[j][i]){swap(eq[i],eq[j]);ans*=-1;break;}}
if(!eq[i][i]){flag=1;return;}int inv=qp(eq[i][i],mod-2);
for(int j=1;j<=en1;j++)if(i!=j&&eq[j][i])
{
int t=1ll*eq[j][i]*inv%mod;if(!t)continue;
for(int k=1;k<=en1;k++)eq[j][k]=(1ll*mod+1ll*eq[j][k]-1ll*eq[i][k]*t)%mod;
}
}
for(int i=1;i<=en1;i++)ans=1ll*ans*eq[i][i]%mod;
}
int main()
{
scanf("%d%d%d",&n,&m,&mod);
for(int i=1,u,v1;i<=m;i++)scanf("%d%d",&u,&v1),add(u,v1),out[u]++,in[v1]++;
for(int i=1;i<=n;i++){if(in[i]==0)S[++en1]=i,top[++en]=i,f[i][i]=1;if(out[i]==0)T[++en2]=i;}
while(be<en)
{
int x=top[++be];for(int i=info[x];i;i=nex[i]){in[v[i]]--;if(!in[v[i]])top[++en]=v[i];}
for(int i=1;i<=en1;i++)for(int j=info[x];j;j=nex[j])(f[S[i]][v[j]]+=f[S[i]][x])%=mod;
}
for(int i=1;i<=en1;i++)for(int j=1;j<=en2;j++)eq[i][j]=f[S[i]][T[j]];
ans=1;Gauss();
printf("%d",flag?0:(ans+mod)%mod);
}
每条边都有一定概率p∈[0,1]出现在图中
求生成一棵树的概率是多少
答案应该是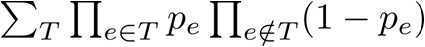 (原谅我不会数学公式)
(原谅我不会数学公式)
即在生成树中的边出现的概率乘上不在生成树中的边不出现的概率
由变元矩阵树定理,矩阵树定理求的是权值积的和,即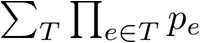
接下来我们想如何把那些不选其它边的概率一起计算了,
即用在生成树上的边的一些信息表示不在生成树上的边不出现的概率。
注意到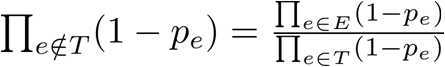 ,显然上面那个分子对于每组数据来说是个常数。
,显然上面那个分子对于每组数据来说是个常数。
所以答案可以变换为
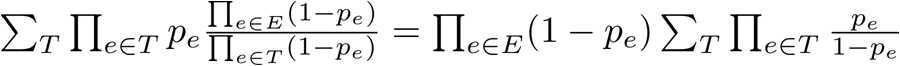
然后就可以用矩阵树定理做了
注意处理当pe=1的情况,赋值成一个很接近1的数就好了
代码
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
const double eps=1e-7;
int n;double mart[55][55],ans=1.0;
bool no(double x){return fabs(x)<eps;}
double Gauss()
{
double ret(1.0);int N(n-1),f(0);
for(int i=1;i<=N;i++)
{
if(no(mart[i][i])){for(int j=i+1;j<=N;j++)if(!no(mart[j][i])){swap(mart[i],mart[j]);f^=1;break;}}
if(no(mart[i][i]))return 0.0;
for(int j=1;j<=N;j++)if(i!=j)
{
double t=mart[j][i]/mart[i][i];
for(int k=1;k<=N;k++)mart[j][k]-=mart[i][k]*t;
}
ret*=mart[i][i];
}
if(f)ret=-ret;
return ret;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%lf",&mart[i][j]);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
{
if(no(mart[i][j]))mart[i][j]=eps;
if(no(1-mart[i][j]))mart[i][j]=1.0-eps;
if(i<j)ans*=1.0-mart[i][j];
mart[i][j]/=(1.0-mart[i][j]);
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
if(i!=j)mart[i][i]+=mart[i][j],mart[i][j]=-mart[i][j];
ans*=Gauss();
printf("%.10lf\n",ans);
}
a0 = A0
ai = ai-1*AX+AY
b0 = B0
bi = bi-1*BX+BY
AoD(n)=\sum_{i=0}^{n-1} aibi
答案mod 1e9+7
n<=10^18,其他数(A0,AX,AY,B0,BX,BY)<=2*10^9
看到n的范围就容易想到矩阵快速幂,来考虑一下如何转移
求AoD(n)需要AoD(n-1)和anbn,所以这两项必须有
而求anbn,因为矩阵乘法原始矩阵各项之间只能相加,
所以anbn只能由an-1bn-1转移来。
anbn=(an-1*Ax+Ay)*(bn-1*Bx+By)
=Ax*Bx*an-1bn-1+AxBy*an-1+AyBx*bn-1+AyBy
所以还需要一个常数项1,an,bn,转移矩阵用Ax,Ay,Bx,By,1来填就好了
代码(压行压得像篇英语作文似的)
#include<cstdio>
#include<cstring>
const int mod=1000000007;
long long n,A0,B0,Ax,Bx,Ay,By;
struct node{long long mart[10][10];}ans,g;
node operator *(node a,node b)
{
node c;memset(c.mart,0,sizeof c.mart);
for(int i=1;i<=5;i++)for(int j=1;j<=5;j++)for(int k=1;k<=5;k++)
(c.mart[i][j]+=1ll*a.mart[i][k]*b.mart[k][j]%mod)%=mod;
return c;
}
int main()
{
while(scanf("%lld%lld%lld%lld%lld%lld%lld",&n,&A0,&Ax,&Ay,&B0,&Bx,&By)!=EOF)
{
if(n==0){printf("0\n");continue;}
memset(g.mart,0,sizeof g.mart);memset(ans.mart,0,sizeof ans.mart);
g.mart[1][1]=1;g.mart[2][1]=Ax*Bx%mod;g.mart[3][1]=Ax*By%mod;g.mart[4][1]=Ay*Bx%mod;g.mart[5][1]=Ay*By%mod;
g.mart[2][2]=Ax*Bx%mod;g.mart[3][2]=Ax*By%mod;g.mart[4][2]=Ay*Bx%mod;g.mart[5][2]=Ay*By%mod;
g.mart[3][3]=Ax%mod;g.mart[5][3]=Ay%mod;g.mart[4][4]=Bx%mod;g.mart[5][4]=By%mod;g.mart[5][5]=1;
ans.mart[1][1]=A0*B0%mod;ans.mart[1][2]=A0*B0%mod;ans.mart[1][3]=A0%mod;ans.mart[1][4]=B0%mod;ans.mart[1][5]=1;
n--;
while(n)
{
if(n&1)ans=ans*g;
n>>=1;g=g*g;
}
printf("%lld\n",ans.mart[1][1]);
}
}
标签:time 逆序数 pre == flag ack 条件 http 今天
原文地址:https://www.cnblogs.com/firecrazy/p/11441448.html