标签:相关 而且 部分 优化 偏差 tar 去掉 机器 分类
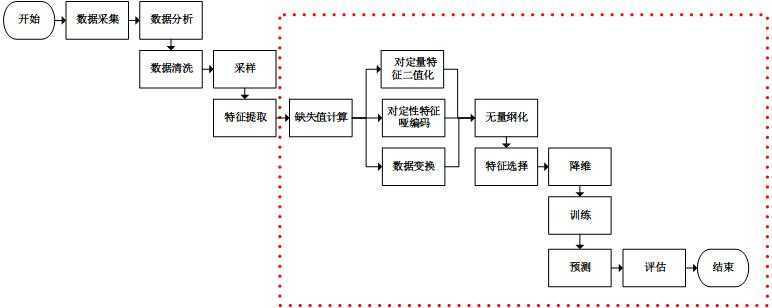
数据清洗:
1、异常值
1)基于概率分布,构建一个概率分布模型,并计算对象符合该模型的概率,把具有低概率的对象视为异常点。
2)聚类,比如我们可以用KMeans聚类将训练样本分成若干个簇,如果某一个簇里的样本数很少,而且簇质心和其他所有的簇都很远,那么这个簇里面的样本极有可能是异常特征样本了。我们可以将其从训练集过滤掉。
3)异常点检测方法,主要是使用iForest或者one class SVM,使用异常点检测的机器学习算法来过滤所有的异常点。
2、数据不均衡
权重法:对不同类别分错的权重不同,或者对样本点的权重不一样;
采样法:1)子采样;2)过采样:对少数类重复;
一分类:对于正负样本极不平衡,重点不在于捕捉类间差别,而是为其中一类建模(YES/NO)
阈值移动:如分类器映射$f(x)\rightarrow [0,1]$,对于某个阈值t,$f(x)\geq t$的样本为正,对t进行调节;
人工合成:对于某一个缺少样本的类别,它会随机找出几个该类别的样本,再找出最靠近这些样本的若干个该类别样本,组成一个候选合成集合,然后在这个集合中不停的选择距离较近的两个样本,在这两个样本之间,比如中点,构造一个新的该类别样本。
数据预处理:
单个特征
1、特征归一化:
原因:
消除指标之间的量纲影响,使各指标处于同一量级,提高训练速度(不会使量级较大的那边影响更大,梯度下降超最低点下降更快);
让数据处于同样的分布,提升泛化能力;
减小累积误差,前几层发生微小改变,后几层就会累积放大,训练过程中一直发生变化,会影响训练速度;
方法:
z-score标准化:基本所有的线性模型在拟合的时候都会做 z-score标准化。具体的方法是求出样本特征x的均值mean和标准差std,然后用(x-mean)/std来代替原特征。这样特征就变成了均值为0,方差为1了。在sklearn中,我们可以用StandardScaler来做z-score标准化。
max-min归一化:也称为离差标准化,预处理后使特征值映射到[0,1]之间。具体的方法是求出样本特征x的最大值max和最小值min,然后用(x-min)/(max-min)来代替原特征。如果我们希望将数据映射到任意一个区间[a,b],而不是[0,1],用(x-min)(b-a)/(max-min)+a来代替原特征即可。在sklearn中,我们可以用MinMaxScaler来做max-min标准化。这种方法的问题就是如果测试集或者预测数据里的特征有小于min,或者大于max的数据,会导致max和min发生变化,需要重新计算。所以实际算法中, 除非你对特征的取值区间有需求,否则max-min标准化没有 z-score标准化好用。
L1/L2范数标准化:如果我们只是为了统一量纲,那么通过L2范数整体标准化也是可以的,具体方法是求出每个样本特征向量的L2范数$\left \|\vec{x} \right \|_{2}$,再用$\vec{x}/\left \|\vec{x} \right \|_{2}$代替。通常情况下,范数标准化首选L2范数标准化。在sklearn中,我们可以用Normalizer来做L1/L2范数标准化。
2、离散化
1)根据阈值进行分组,比如我们根据连续值特征的分位数,将该特征分为高,中和低三个特征。将分位数从0-0.3的设置为高,0.3-0.7的设置为中,0.7-1的设置为高。
2)用GBDT:用训练集的所有连续值和标签输出来训练GBDT,最后得到的GBDT模型有两颗决策树,第一颗决策树有三个叶子节点,第二颗决策树有4个叶子节点。如果某一个样本在第一颗决策树会落在第二个叶子节点,在第二颗决策树落在第4颗叶子节点,那么它的编码就是0,1,0,0,0,0,1,一共七个离散特征,其中会有两个取值为1的位置,分别对应每颗决策树中样本落点的位置。在sklearn中,我们可以用GradientBoostingClassifier的 apply方法很方便的得到样本离散化后的特征,然后使用独热编码即可。(LR+GBDT)
3)one-hot:比如某特征的取值是高,中和低,那么我们就可以创建三个取值为0或者1的特征,将高编码为1,0,0这样三个特征,中编码为0,1,0这样三个特征,低编码为0,0,1这样三个特征。也就是说,之前的一个特征被我们转化为了三个特征。sklearn的OneHotEncoder可以帮我们做这个处理。
4)dummy coding虚拟编码,它和独热编码类似,但是它的特点是,如果我们的特征有N个取值,它只需要N-1个新的0,1特征来代替,而独热编码会用N个新特征代替。比如一个特征的取值是高,中和低,那么我们只需要两位编码,比如只编码中和低,如果是1,0则是中,0,1则是低。0,0则是高了。目前虚拟编码使用的没有独热编码广,因此一般有需要的话还是使用独热编码比较好。
3、连续化
1)one-hot
2)特征嵌入embedding:一般用于深度学习中。比如对于用户的ID这个特征,如果要使用独热编码,则维度会爆炸,如果使用特征嵌入就维度低很多了。对于每个要嵌入的特征,我们会有一个特征嵌入矩阵,这个矩阵的行很大,对应我们该特征的数目。比如用户ID,如果有100万个,那么嵌入的特征矩阵的行就是100万。但是列一般比较小,比如可以取20。这样每个用户ID就转化为了一个20维的特征向量。进而参与深度学习模型。在tensorflow中,我们可以先随机初始化一个特征嵌入矩阵,对于每个用户,可以用tf.nn.embedding_lookup找到该用户的特征嵌入向量。特征嵌入矩阵会在反向传播的迭代中优化。
4、缺失值
如果是连续值:1)平均值来填充缺失值,2)取中位数来填充缺失值。
如果是离散值,众数来填充缺失值。
在sklearn中,可以使用preprocessing.Imputer来选择这三种不同的处理逻辑做预处理。
利用机器学习方法,将缺失属性作为预测目标进行预测,具体为将样本根据是否缺少该属性分为训练集和测试集,然后采用如回归、决策树等机器学习算法训练模型,再利用训练得到的模型预测测试集中样本的该属性的数值。这个方法根本的缺陷是如果其他属性和缺失属性无关,则预测的结果毫无意义;但是若预测结果相当准确,则说明这个缺失属性是没必要纳入数据集中的;一般的情况是介于两者之间。
多个特征
1、组合特征
在我们拿到已有的特征后,我们还可以根据需要寻找到更多的高级特征。比如有车的路程特征和时间间隔特征,我们就可以得到车的平均速度这个二级特征。根据车的速度特征,我们就可以得到车的加速度这个三级特征,根据车的加速度特征,我们就可以得到车的加加速度这个四级特征。。。也就是说,高级特征可以一直寻找下去。一般采取特征间的加减乘除等;
2、特征选择
1、特征来源:1)收集到的特征;2)寻找高级特征
2、特征选择
1)过滤法:按照特征的发散性或者相关性指标对各个特征进行评分,设定评分阈值或者待选择阈值的个数,选择合适特征。
首先,方差小说明提供的信息少,作为特征选择标准。
方差越大的特征,那么我们可以认为它是比较有用的。
如果方差较小,比如小于1,那么这个特征可能对我们的算法作用没有那么大。
最极端的,如果某个特征方差为0,即所有的样本该特征的取值都是一样的,那么它对我们的模型训练没有任何作用,可以直接舍弃。
在实际应用中,我们会指定一个方差的阈值,当方差小于这个阈值的特征会被我们筛掉。sklearn中的VarianceThreshold类可以很方便的完成这个工作。
??那均值方差标准化的时候把方差都调成一样的,改变了分布,合理吗?
**首先,z-score标准化是一种线性变换,将数据按比例缩放,并不影响数值之间的关系,然后,预测的是特征与目标之间的概率分布,而不是特征本身的概率分布;学习的目标是几个特征的联合分布拟合靠近目标值。
from sklearn.feature_selection import VarianceThreshold #方差选择法,返回值为特征选择后的数据 #参数threshold为方差的阈值 VarianceThreshold(threshold=3).fit_transform(iris.data)
这个主要用于输出连续值的监督学习算法中。我们分别计算所有训练集中各个特征与输出值之间的相关系数,设定一个阈值,选择相关系数较大的部分特征。
from sklearn.feature_selection import SelectKBest from scipy.stats import pearsonr #选择K个最好的特征,返回选择特征后的数据 #第一个参数为计算评估特征是否好的函数,该函数输入特征矩阵和目标向量,输出二元组(评分,P值)的数组,数组第i项为第i个特征的评分和P值。在此定义为计算相关系数 #参数k为选择的特征个数 SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
一般采用卡方分布,用于离散型特征;
F检验在数据服从正态分布时效果会非常稳定,因此如果使用F检验过滤,我们会先将数据转换成服从正态分布的方式。F检验的本质是寻找两组数据之间的线性关系,其原假设是”数据不存在显著的线性关系“。它返回F值和p值两个统计量。和卡方过滤一样,我们希望选取p值小于0.05或0.01的特征,这些特征与标签时显著线性相关的,而p值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征,应该被删除。
https://segmentfault.com/a/1190000003719712
x2用于衡量实际值与理论值的差异程度,包含了以下两个信息:1)实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的);2)差异程度与理论值的相对大小;
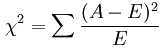
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 #选择K个最好的特征,返回选择特征后的数据 SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
从信息熵的角度分析各个特征和输出值之间的关系评分。互信息值越大,说明该特征和输出值之间的相关性越大,越需要保留。在sklearn中,可以使用mutual_info_classif(分类)和mutual_info_regression(回归)来计算各个输入特征和输出值之间的互信息。
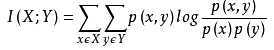
from sklearn.feature_selection import SelectKBest
from minepy import MINE
#由于MINE的设计不是函数式的,定义mic方法将其为函数式的,返回一个二元组,二元组的第2项设置成固定的P值0.5
def mic(x, y):
m = MINE()
m.compute_score(x, y)
return (m.mic(), 0.5)
#选择K个最好的特征,返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
2)包装法:根据目标函数,通常是预测效果评分,每次选择部分特征,或者排除部分特征。
递归消除特征法使用一个机器学习模型来进行多轮训练,每轮训练后,消除若干权值系数的对应的特征,再基于新的特征集进行下一轮训练。在sklearn中,可以使用RFE函数来选择特征。
最先消除对损失函数影响最小的那个特征;
我们下面以经典的SVM-RFE算法来讨论这个特征选择的思路。这个算法以支持向量机来做RFE的机器学习模型选择特征。它在第一轮训练的时候,会选择所有的特征来训练,得到了分类的超平面wx+b=0后,如果有n个特征,那么RFE-SVM会选择出ww中分量的平方值wi最小的那个序号i对应的特征,将其排除,在第二类的时候,特征数就剩下n-1个了,我们继续用这n-1个特征和输出值来训练SVM,同样的,去掉w2iwi2最小的那个序号i对应的特征。以此类推,直到剩下的特征数满足我们的需求为止。
from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression #递归特征消除法,返回特征选择后的数据 #参数estimator为基模型 #参数n_features_to_select为选择的特征个数 RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
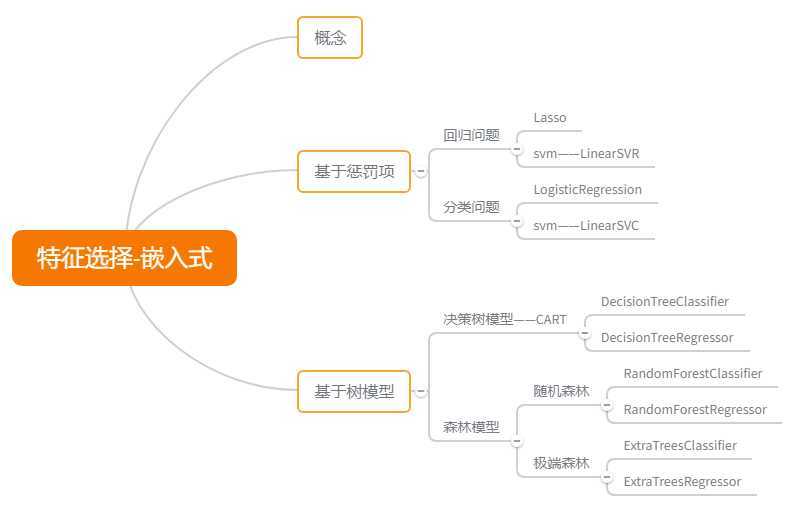
3)嵌入法:先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小来选择特征。类似于过滤法,但是它是通过机器学习训练来确定特征的优劣,而不是直接从特征的一些统计学指标来确定特征的优劣。
最常用的是使用L1正则化和L2正则化来选择特征。正则化惩罚项越大,那么模型的系数就会越小。当正则化惩罚项大到一定的程度的时候,部分特征系数会变成0,当正则化惩罚项继续增大到一定程度时,所有的特征系数都会趋于0. 但是我们会发现一部分特征系数会更容易先变成0,这部分系数就是可以筛掉的。也就是说,我们选择特征系数较大的特征。常用的L1正则化和L2正则化来选择特征的基学习器是逻辑回归。
在sklearn中,使用SelectFromModel函数来选择特征。
此外也可以使用决策树或者GBDT。一般来说,可以得到特征系数coef或者可以得到特征重要度(feature importances)的算法才可以做为嵌入法的基学习器。
from sklearn.feature_selection import SelectFromModel from sklearn.ensemble import GradientBoostingClassifier #GBDT作为基模型的特征选择 SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)
3、降维
PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
1、主成分分析法(PCA)
from sklearn.decomposition import PCA #主成分分析法,返回降维后的数据 #参数n_components为主成分数目 PCA(n_components=2).fit_transform(iris.data)
2、线性判别分析法(LDA)
from sklearn.lda import LDA #线性判别分析法,返回降维后的数据 #参数n_components为降维后的维数 LDA(n_components=2).fit_transform(iris.data, iris.target)
标签:相关 而且 部分 优化 偏差 tar 去掉 机器 分类
原文地址:https://www.cnblogs.com/danniX/p/10606286.html