标签:hellip image 单位 不同的 sub 编写 div 在线 ken
在规定条件下,规定时间内,软件不引起系统失效的概率
软件系统在规定的时间内以及规定的环境条件下,完成规定功能的能力
预测软件在实际运行中的可靠性,同时通过测试可以提高整个软件的防错、容错和纠错的能力
计算机系统的可靠性是制从它开始运行(t=0)到某时刻t这段时间内能正常运行的概率,用R(t)表示。
失效率是指单位时间内失效的元件数与元件总数的比例,以λ表示,当λ为常数时,可靠性与失效率的关系为: R(t)=е^(-λt)。
| 系统类型 | 可靠性 | 失效率 |
| 串联系统 | R=R1×R2×...×Rn | λ=λ1+λ2+...+λn |
| 并联系统 | R=1-(1-R1)×(1-R2)×...×(1-Rn) | 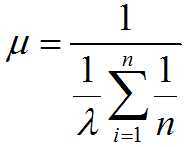 |
| 模冗余系统 | |
|
1)串联系统:假设一个系统由n个子系统组成,当且仅当所有的子系统都有能正常工作时,系统才能正常工作,这种系统称为串联系统
设系统各个子系统的可靠性分别用R1, R2, R3……, Rn表示,则系统的可靠性
R=R1×R2×R3×……×Rn
如果系统的各个子系统的失效率分别用λ1, λ2, λ3……, λn来表示,则系统的失效率
λ=λ1+λ2+λ3+……+λn
则系统平均故障间隔时间为:
MTBF=1/λ
假设本题三个子系统是串联的,n=3,R1=R2=R3=0.9,λ1=λ2=λ3=1/10000=0.0001,则:
系统可靠性 R= R1×R2×R3=0.9×0.9×0.9=0.729
系统失效率 λ=λ1+λ2+λ3=0.0001+0.0001+0.0001=0.0003
系统平均故障间隔时间 MTBF=1/0.0003=3333
(2)并联系统:假如一个系统由n个子系统组成,只要有一个子系统能够正常工作,系统就能正常工作。
设系统各个子系统的可靠性分别用R1, R2, R3……, Rn表示,则系统的可靠性
R=1-(1-R1)×(1-R2)×(1-R3)×……×(1-Rn)
如果系统的各个子系统的失效率均为λ,则系统的失效率μ为
则系统平均故障间隔时间为:
MTBF= 1/μ
根据本题题意可知,n=3,R1=R2=R3=0.9,λ1=λ2=λ3=1/10000=0.0001,则:
系统可靠性 R = (1-R1)×(1-R2)×(1-R3)=1-(1-0.9)×(1-0.9)×(1-0.9)=0.999
系统失效率 μ = 1/((1/0.0001)*(1/1+1/2+1/3))=6/(10000*11)
系统平均故障间隔时间 MTBF=10000*11/6=18333
失效模式影响分析,严酷性分析,故障树分析和潜在线路分析
确定可靠性目标,进行软件运行剖面,编写可靠性用例,执行测试,分析测试结果
软件运行剖面
MUSA软件分析的原则:
1. 模式剖面:对软件的使用者进行分类,根据对使用者的划分将软件划分成不同的模式剖面
2. 功能剖面:根据每个模式下的功能可以划分为不同的功能剖面
3. 运行剖面:每一个功能由许多运行组成。这些运行的集合便构成了运行剖面
标签:hellip image 单位 不同的 sub 编写 div 在线 ken
原文地址:https://www.cnblogs.com/leslie12956/p/11442862.html