搜索入门练习题6 马的遍历 题解

标签：表示   http   开始   code   策略   tar   扩展   pre   cout   

题目出处：《信息学奥赛一本通》例5.5

题目描述

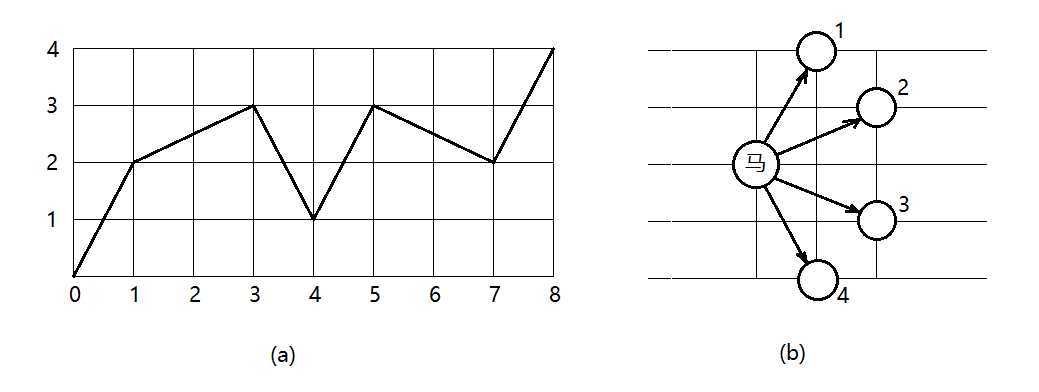
中国象棋半张棋盘如图（a）所示。马自左下角往右上角跳。今规定只许往右跳，不许往左跳。比如（a）中所示为一种跳行路线，并将所经路线打印出来。打印格式为：

0,0->2,1->3,3->1,4->3,5->2,7->4,8……

提示：马每一步最多有 \(4\) 个方向可以走，如图（b）所示。

输出格式

输出马行走的所有方案，每个方案按照题目描述占一行。

题目分析

使用深度优先搜索可以解决这个问题。
如图（b）所示，马最多有四个方向，若原来的横坐标为 \(j\) 、纵坐标为 \(i\) ，则四个方向的移动可表示为：

• 1： \((i,j) \rightarrow (i+2,j+1)\) ； \((i \lt 3,j \lt 8)\)
• 2： \((i,j) \rightarrow (i+1,j+2)\) ； \((i \lt 4,j \lt 7)\)
• 3： \((i,j) \rightarrow (i-1,j+2)\) ； \((i \gt 0,j \lt 7)\)
• 4： \((i,j) \rightarrow (i-2,j+1)\) ； \((i \gt 1, j \lt 8)\)

深度优先搜索的搜索策略可以有很多种，但本质还是状态之间的转换。
我们用 \((i,j)\) 表示横坐标为 \(j\) ，纵坐标为 \(i\) 时的马的状态。一开始马在 \((0,0)\) ，它最终要走到 \((4,8)\) 。
因为马每次最少往右边走一格，所以马行走的步数最多八步。我们开两个数组 ansx[] 和 ansy[] 来存储马每一步的状态，一开始ansx[0] = ansy[0] = 0，表示第 \(0\) 步的时候马处在 \((0,0)\) 位置，我们使用函数 f(int id) 用于表示第 id 步时马的放置方案。
如果马此时的放置位置 \((x,y)\) 满足 \(y = 8\)的条件，那么我们：

• 看一下 \(x\) 是不是等于 \(4\) ，如果是的话则说明走到了终点，输出方案；
• 否则就说明马走到最右边的格子但不是 \((4,8)\) ，说明这条路不可行，返回。

如果 \(y \lt 8\) ，说明还没有走到最右边，继续扩展新的状态。
实现代码如下：

#include <bits/stdc++.h>
using namespace std;
// (ansx[i],ansy[i])用于记录第i步的状态
// dir数组用于表示马要行走的四个方向
int ansx[9], ansy[9];
int dir[4][2] = { 2, 1, 1, 2, -1, 2, -2, 1 };
// in_map函数用于确定(x,y)是否超出了棋盘边界
bool in_map(int x, int y) {
    return x >= 0 && x <= 4 && y >= 0 && y <= 8;
}
// output函数用于从第0步输出到第id步的方案
void output(int id) {
    cout <<"0,0";
    for (int i = 1; i <= id; i ++)
        cout << "->" << ansx[i] << "," << ansy[i];
    cout << endl;
}
// f函数用于搜索遍历所有的方案
void f(int id) {
    int x1 = ansx[id], y1 = ansy[id];   // (x1, y1) 用于表示当前马的状态
    if (y1 == 8) {  // 说明已经到达最右边的那一列了
        if (x1 == 4) {  // 说明走到了终点 (4,8)
            output(id);
        }
        // else // 其他情况不用输出，直接退出就可以了
        return;
    }
    for (int i = 0; i < 4; i ++) {  // 遍历4个方向
        int x2 = x1 + dir[i][0];
        int y2 = y1 + dir[i][1];    // (x2,y2)是(x1,y1)能走到的4个点之一
        if (in_map(x2,y2)) {
            ansx[id+1] = x2;  // 将ansx[id+1]更新为x2
            ansy[id+1] = y2;  // 将ansy[id+1]更新为y2
            f(id+1);        // 设置到第id+1步再进f(id+1)去设置第id+2步
        }
    }
}
int main() {
    f(0); // 从(0,0)开始扩展状态
    return 0;
}

注意：我这里是按照图（b）中1、2、3、4的顺序优先走的，实际搜索是按照相关规则就该程序中的dir数组即可。

搜索入门练习题6 马的遍历 题解

标签：表示   http   开始   code   策略   tar   扩展   pre   cout   

原文地址：https://www.cnblogs.com/zifeiynoip/p/11450708.html