2019 宁夏网络赛

时间：2019-09-03 21:55:44 阅读：102 评论：0 收藏：0 [点我收藏+]

标签：inno splay ali pow letters Helm child algorithm break

A、Maximum Element In A Stack

As an ACM-ICPC newbie, Aishah is learning data structures in computer science. She has already known that a stack, as a data structure, can serve as a collection of elements with two operations:

push, which inserts an element to the collection, and
pop, which deletes the most recently inserted element that has not yet deleted.

Now, Aishah hopes a more intelligent stack which can display the maximum element in the stack dynamically. Please write a program to help her accomplish this goal and go through a test with several operations.

Aishah assumes that the stack is empty at first. Your program will output the maximum element in the stack after each operation. If at some point the stack is empty, the output should be zero.

Input

The input contains several test cases, and the first line is a positive integer

To avoid unconcerned time consuming in reading data, each test case is described by seven integers $\le n \le 5 \times 10^6),p,q,m(1 \le p,q,m \le 10^9),SA,SB \ and \ SC(10^4 \le SA,SB,SC \le 10^6)n(1≤n≤5×106),p,q,m(1≤p,q,m≤109),SA,SB and SC(104≤SA,SB,SC≤106). Theinteger nnis the number of operations, and your program should generate all operations using the following code in C++.$

 
 
 
 
 

int n, p, q, m;

unsigned int SA, SB, SC;
unsigned int rng61() {
    SA ^= SA << 16;
    SA ^= SA >> 5;
    SA ^= SA << 1;
    unsigned int t = SA; SA = SB;
    SB = SC;
    SC ^= t ^ SA;
    return SC;
}
void gen(){
    scanf("%d%d%d%d%u%u%u", &n, &p, &q, &m, &SA, &SB, &SC);
    for(int i = 1; i <= n; i++) {
        if(rng61() % (p + q) < p)
            PUSH(rng61() % m + 1);
        else
            POP();
    }
}
 
 

The procedure PUSH(v) used in the code inserts a new element with value v into the stack and the procedure POP( ) pops the topmost element in the stack or does nothing if the stack is empty.

Output

For each test case, output a line containing Case #x: y, where $\oplus^n_{i=1} (i \cdot a_i)⊕i=1n?(i⋅ai?) where a_iai? is the answer after the ii-th operation and \oplus⊕ means bitwise xor.$

输出时每行末尾的多余空格，不影响答案正确性

样例输入

2
4 1 1 4 23333 66666 233333
4 2 1 4 23333 66666 233333

样例输出

Case #1: 19
Case #2: 1

样例解释

The first test case in the sample input has

POP();
POP();
PUSH(1);
PUSH(4).

The second test case also has

PUSH(2);
POP();
PUSH(1);
POP().

#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
#include<math.h>
#include<string>
#include<string.h>
#include<vector>
#include<utility>
#include<map>
#include<queue>
#include<set>
#include<stack>
#define mx 0x3f3f3f3f
#define ll long long
#define MAXN 100
using namespace std;
stack<ll>s;
int n,p,q,m;
ll ans;
unsigned int A, B, C;
unsigned int rng61()
{
    A ^= A << 16;
    A ^= A >> 5;
    A ^= A << 1;
    unsigned int t = A;
    A = B;
    B = C;
    C ^= t ^ A;
    return C;
}
void gen()
{
    scanf("%d%d%d%d%u%u%u",&n,&p,&q,&m,&A,&B,&C);
    for(int i=1;i<=n;i++)
    {
        if(rng61()%(p+q)<p)
        {
            ll temp=rng61()%m+1;
            if(s.size()==0)
                s.push(temp);
            else
                s.push(max(temp,s.top()));
        }
        else
        {
            if(s.size())
                s.pop();
        }
        if(s.size())
            ans^=i*s.top();
    }
} 


int main()
{
    int t;
    cin>>t;
    for(int i=1;i<=t;i++)
    {
        ans=0;
        while(s.size())
            s.pop();
        gen();
        cout<<"Case #"<<i<<": "<<ans<<endl;
    }
    return 0;
}

C、Caesar Cipher

In cryptography, a Caesar cipher, also known as the shift cipher, is one of the most straightforward and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions up (or down) the alphabet.

For example, with the right shift of

技术图片

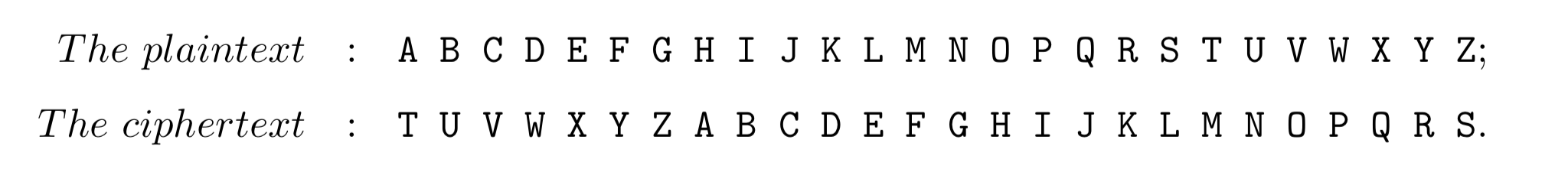
Now you have a plaintext and its ciphertext encrypted by a Caesar Cipher. You also have another ciphertext encrypted by the same method and are asked to decrypt it.

Input

The input contains several test cases, and the first line is a positive integer

For each test case, the first line contains two integers $\le n, m \le 50)m(1≤n,m≤50) indicating the length of the first two texts (a plaintext and its ciphertext) and the length of the third text which will be given. Each of the second line and the third line contains a string only with capital letters of length nn, indicating a given plaintext and its ciphertext respectively. The fourth line gives another ciphertext only with capital letters of length mm.$

We guarantee that the pair of given plaintext (in the second line) and ciphertext (in the third line) is unambiguous with a certain Caesar Cipher.

Output

For each test case, output a line containing Case #x: T, where

输出时每行末尾的多余空格，不影响答案正确性

样例输入

1
7 7
ACMICPC
CEOKERE
PKPIZKC

样例输出

Case #1: NINGXIA

题意：第一行和第二行给你一个翻译样例（明文和密文），让你找翻译规律，第三行给密文，要你按照翻译规律找明文

//密码解密
#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
#include<math.h>
#include<string>
#include<string.h>
#include<vector>
#include<utility>
#include<map>
#include<queue>
#include<set>
#define mx 0x3f3f3f3f
#define ll long long
#define MAXN 100
using namespace std;
string s,ss;
int main()
{
    int n,m,t,k=0;
    cin>>t;
    while(t--)
    {
        k++;
        cin>>n>>m;
        cin>>s>>ss;
        int x=s[0]-ss[0];
        cin>>ss;
        cout<<"Case #"<<k<<": ";
        for(int i=0;ss[i];i++)
            printf("%c",( ss[i] -‘A‘ + x+26  )% 26 +65);
        printf("\n");
    }
    return 0;
}
/*
25 5
UVWXYZ
NOPQRX
TUVWXY
*/

F、Moving On

Firdaws and Fatinah are living in a country with

Firdaws‘s home locates in the city

Input

The input contains several test cases, and the first line is a positive integer

For each test case, the first line contains two integers $\le n \le 200)n(1≤n≤200) which is the number of cities, and q (1 \le q \le 2 \times 10^4)q(1≤q≤2×104) which is the number of queries that will be given. The second line contains nn integers r_1, r_2, \cdots , r_nr1?,r2?,?,rn? indicating the risk of kidnapping or robbery in the city 11 to nn respectively. Each of the following nn lines contains nn integers, the jj-th one in the ii-th line of which, denoted by d_{i,j}di,j?, is the distance from the city iito the city jj.$

Each of the following

We guarantee that $\le r_i \le 10^5, 1 \le d_{i,j} \le 10^5 (i \neq j), d_{i,i} = 01≤ri?≤105,1≤di,j?≤105(i?=j),di,i?=0 and d_{i,j} = d_{j,i}di,j?=dj,i?. Besides, each query satisfies 1 \le u,v \le n1≤u,v≤n and 1 \le w \le 10^51≤w≤105.$

Output

For each test case, output a line containing Case #x: at first, where

输出时每行末尾的多余空格，不影响答案正确性

样例输入

样例输出

Case #1:
0
1
3
0
1
2

题意：输入t，表示t个测试样例
输入n,q,表示n个点，q次询问
下一行n个数表示[1,n]个点的危险值
接下来n行，每行3个数描述一条边，点x到y的距离为z;
最后q行，每行3个数，求从起点U到终点V,在每一个点危险值不超过W的前提下的最短距离

#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
#include<math.h>
#include<string>
#include<string.h>
#include<vector>
#include<utility>
#include<map>
#include<queue>
#include<set>
#define mx 0x3f3f3f3f
#define ll long long
#define MAXN 100
using namespace std;
int dp[250][250][250];//dp[k][i][j]表示 添加(第1~k小的危险值的城市后)的 i->j 最短路
int vis[250],rk[250];
bool cmp(int i,int j)
{
    return rk[i]<rk[j];
}
int main()
{
    int t;
    scanf("%d",&t);
    for(int tt=1;tt<=t;tt++)
    {
        memset(dp,mx,sizeof(dp));
        int n,q;
        scanf("%d%d",&n,&q);
        for(int i=1;i<=n;i++)
        {
            vis[i]=i;//初始化排名
            scanf("%d",&rk[i]);
        }
        sort(vis+1,vis+n+1,cmp);//把城市的编号按风险等级从小到大排序，vis[排名]=编号
        // for(int i=1;i<=n;i++)
        //     cout<<vis[i]<<‘ ‘;
        // cout<<"<-----"<<endl;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                scanf("%d",&dp[0][i][j]);//初始化每一条边的危险等级为0
        for(int k=1;k<=n;k++)
        {
            int now=vis[k];
            for(int i=1;i<=n;i++)
            {
                for(int j=1;j<=n;j++)
                    dp[k][i][j]=min(dp[k-1][i][j],dp[k-1][i][now]+dp[k-1][now][j]); 
            }

        }
        printf("Case #%d:\n",tt);
        for(int i=1;i<=q;i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            int k=0;
            for(int j=1;j<=n;j++)
                if(rk[vis[j]]<=w)//把危险值最接近w的边都加进去之后的最短路
                    k=j;
            printf("%d\n",dp[k][u][v]);
        }
    }
    return 0;
}

H、Fight Against Monsters

It is my great honour to introduce myself to you here. My name is Aloysius Benjy Cobweb Dartagnan Egbert Felix Gaspar Humbert Ignatius Jayden Kasper Leroy Maximilian. As a storyteller, today I decide to tell you and others a story about the hero Huriyyah, and the monsters.

Once upon a time, citizens in the city were suffering from $HP_iHPi?, and its attack value was ATK_iATKi?.$

They fought in a cave through a turn-based battle. During each second, the hero Huriyyah was attacked by monsters at first, and the damage was the sum of attack values of all alive monsters. Then he selected a monster and attacked it. The monster would suffer the damage of

Now, my smart audience, can you calculate the minimum amount of total damages our hero should suffer before he won the battle?

Input

The input contains several test cases, and the first line is a positive integer $10^3103.$

For each test case, the first line contains an integers $\le n \le 10^5)n(1≤n≤105) which is the number of monsters. The ii-th line of the following nn lines contains two integers HP_iHPi? and ATK_i (1 \le HP_i, ATK_i \le 10^5)ATKi?(1≤HPi?,ATKi?≤105) which describe a monster.$

We guarantee that the sum of $10^6106.$

Output

For each test case, output a line containing Case #x: y, where

输出时每行末尾的多余空格，不影响答案正确性

样例输入

样例输出

Case #1: 19
Case #2: 14


题意：猎人打怪兽，怪兽有一个生命值和攻击值，猎人的攻击值在打不同的怪兽时从1开始随攻击次数递增
攻击顺序时所有怪兽先攻击猎人一次，猎人在选择一个怪兽进行攻击
问：猎人杀死所有怪兽，最少需要多少生命值

题解：贪心排序，按照每个怪兽对猎人造成的总伤害（总伤害=攻击力*攻击次数）从大到小进行排序，猎人先把总伤害高的怪兽杀死

//贪心打怪
#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
#include<math.h>
#include<string>
#include<string.h>
#include<vector>
#include<utility>
#include<map>
#include<queue>
#include<set>
#include<stack>
#define mx 0x3f3f3f3f
#define ll long long
#define MAXN 100
using namespace std;
struct node
{
    ll hp;
    ll ak;
    ll cnt;
}p[100005];
bool cmp(node a,node b)
{
    return a.ak*b.cnt>b.ak*a.cnt;
}
ll check(ll x)
{
    ll temp=x,num=0;
    for(int i=1;i<=temp;i++)
    {
        if(x>0)
            num++;
        else
            break;
        x=x-i;
    }
    return num;
}
int main()
{
    ll t,n,sum;
    scanf("%lld",&t);
    for(int j=1;j<=t;j++)
    {
        sum=0;
        scanf("%lld",&n);
        for(int i=0;i<n;i++)
        {
            scanf("%lld%lld",&p[i].hp,&p[i].ak);
            p[i].cnt=check(p[i].hp);
            sum=sum+p[i].ak;
        }
        sort(p,p+n,cmp);
        ll ans=0;
        for(int i=0;i<n;i++)
        {
            ans=ans+p[i].cnt*sum;
            sum=sum-p[i].ak;
        }
        printf("Case #%d: %lld\n",j,ans);
    }
}

2019 宁夏网络赛

标签：inno splay ali pow letters Helm child algorithm break

原文地址：https://www.cnblogs.com/-citywall123/p/11455611.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

2019 宁夏网络赛

A、Maximum Element In A Stack

Input

Output

样例输入复制

样例输出复制

样例解释

C、Caesar Cipher

Input

Output

样例输入复制

样例输出复制

F、Moving On

Input

Output

样例输入复制

样例输出复制

H、Fight Against Monsters

Input

Output

样例输入复制

样例输出复制

样例输入

样例输出

样例输入

样例输出

样例输入

样例输出

样例输入

样例输出