标签:目的 ati for 行号 代码 stat print 取绝对值 span
今天在回顾JavaSE时,又见到了曾经练习的小例子,用【*】输出一个菱形。如图
* *** ***** *** *
图1
按照自己以前的逻辑肯定会选择一半一半的输出,如先输出上面一个锥形,再输出下面一个锥形。如果要输出一个矩阵的数据的话,如图2,还会选择先输出【@】,再输出【*】,再输出【@】。
这里为方便显示,把空格替换成了【@】。
@@@*@@@ @@***@@ @*****@ ******* @*****@ @@***@@ @@@*@@@
图2
代码如下:
1 public static void test2(int rowC) { 2 int i,j,k,l; 3 int midNum = rowC/2 + 1; 4 for(i=1;i<=midNum;i++){ 5 6 for(j=1;j<=midNum-i;j++) 7 System.out.print("@"); 8 9 for(k=1;k<=2*i-1;k++) 10 System.out.print("*"); 11 12 for(l=1;l<=rowC-j-k+2;l++) 13 System.out.print("@"); 14 15 System.out.print("\n"); 16 17 } 18 19 for(i=1;i<=midNum-1;i++){ 20 21 for(j=1;j<=i;j++) 22 System.out.print("@"); 23 24 for(k=1;k<=rowC-2*i;k++) 25 26 System.out.print("*"); 27 28 for(l=1;l<=rowC-j-k+2;l++) 29 System.out.print("@"); 30 31 System.out.println(); 32 33 } 34 }
算法思想就是先找的中间行,然后从第一行输出到中间行。这过程中呢,有依次输出了【@】,【*】,【@】。
最后输出下半部分的时候,也是如此。有没有发现,看着挺简单的,就是码的时候麻烦,而且重复的太多,想要改变输出的字符时,改动又大。于是乎,博主就想有没有一种算法可以,尽量少的代码来实现它。
于是乎,就开始研究输出行跟输出字符个数的关系,(就是像研究数列一样的东西了)。
最开始我是想在一次列循环中,就把【@】【*】全部输出成理想形式 如,@@@*@@@。
第一步,找出每行输出【*】的个数 1,3,5,7,5,3,1。这种对称形式的数据组合。
第二步,找出每行输出【*】时的开始位置和结束位置。
开始 结束
第1行:4 4
第2行:3 5
第3行:2 6
第4行:1 7
第5行:2 6
第6行:3 5
第7行:4 4
有没有发现都是对称形式的数列。
第三步,找出输出行与上面的数列的关系。
开始 结束 【*】个数
第1行:4 4 1
第2行:3 5 3
第3行:2 6 5
第4行:1 7 7
第5行:2 6 5
第6行:3 5 3
第7行:4 4 1
首先,我们发现 (1) 结束 - 开始 + 1 = 【*】个数
(2)总行数 - 2 * | 中间列号 - 当前行 | = 【*】个数 (ps:因为7行7列,所以中间列号是4。 | | 代表取绝对值 )
(3)开始 = | 中间列号 - 当前行 | + 1
总结出上面三个等式之后,我觉得可以列方程求解了。
假设:开始为x, 结束为y,(主要目的就是算出开始和结束位置,那之后,在一次列循环中就可以输出最终结果)
当前行为j, 总行数为 A, 中间列号为 midNum
【1】 y - x + 1= A - 2 * | midNum - j |
【2】 x = | midNum - j | + 1
然后【2】式代入【1】则,y = A - | midNum - j |
我们知道midNum 和 A 的值, 分别是 4 和 7,那么x,y的值就会用当前行号来确定了。就可以编程了。呵呵。
代码如下:
public static void test1(int rowC) { int midNum = rowC/2 + 1; for(int j = 1; j <= rowC; j++) { for(int i = 1; i <= rowC; i++) { if(i >= (Math.abs(midNum-j) + 1) && (i <= (rowC-Math.abs(midNum-j)))) { System.out.print("*"); }else { System.out.print("@"); } } System.out.println(); } }
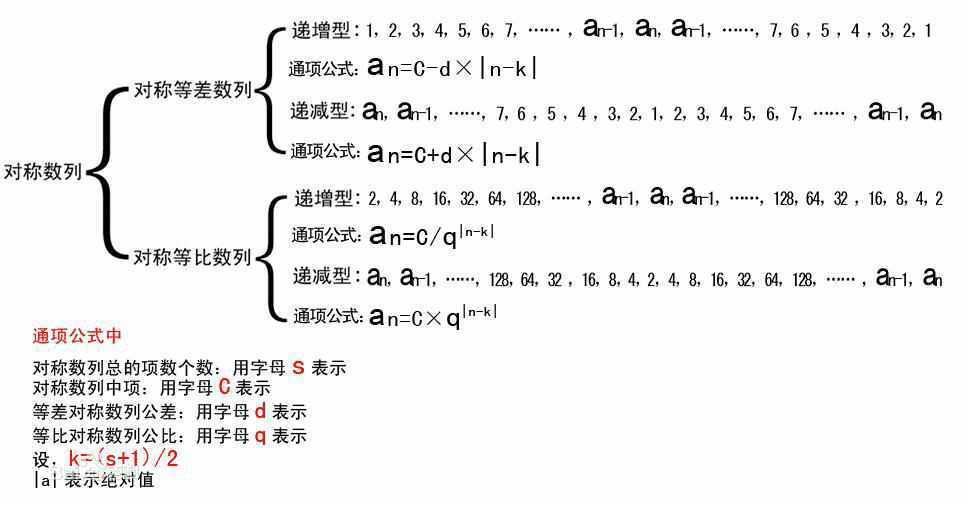
是不是感觉比第一种少了不少代码。其实这其中运用了对称数列的知识(ps:我也是研究完了,网上百度对称数列通项才清楚,自己推算的正是它的通项公式)。
如下图所示,每行输出【*】个数:1,3,5,7,5,3,1 就是一个等差为2的递增型对称等差数列。通项公式中的n就是当前行号,对称中项 C,是跟总行数A一样的值。k就是中间项的下标(A/2+1)或(A+1)/2。
标签:目的 ati for 行号 代码 stat print 取绝对值 span
原文地址:https://www.cnblogs.com/leafIcesun/p/11456363.html