标签：for   等于   col   识别   mit   拆分   模式   最快   函数   

特征提取

直方图

• 用于计算图片的特征（Feature) 和表达（representation）
• 对图片数据/特征分别的一种统计
  ** 灰度、颜色
  ** 梯度/边缘、形状、纹理
  ** 局部特征点、视觉词汇
• 区间（bin）
  ** 均有一定的统计或者物理意义
  ** 一种数据或者特征的代表
  ** 需要预定义或者基于数据进行学习
  ** 数值是一种统计量： 概率、频数、特定积累
• 维度小于原始数据

对数据空间（Bin）进行量化

• 人工分割

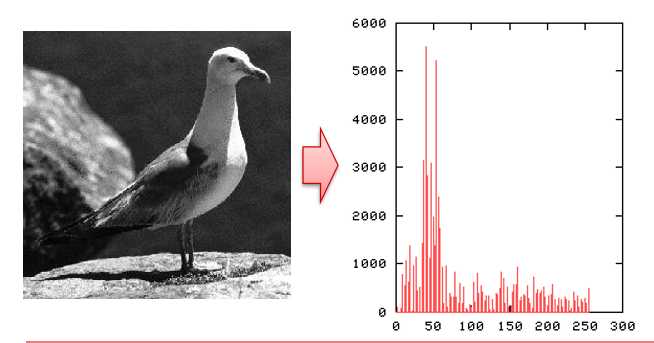
人工分割：简单高效，但是存在量化问题，量化过宽容易造成精度的损失或者量化过窄容易过拟合

• 聚类算法进行无监督学习
  常用方法：Kmeans、 EM算法、Mean shift、谱聚类、层次聚类等
• Kmeans 容易受到类中心书K的选择和初始点的选取的影响-->容易陷入局部最优
  ** 改进：多次全随机取最优；Kmeans++ 半随机

几何特征

• 边缘（Edge）
  ** 像素明显变化的区域
  ** 具有丰富的语义信息
  用于物体识别和几何、视角变化
  一般边缘定义为：像素值函数快速变化的区域-->一阶导数（灰度值函数）的极值区域

• 边缘提取：
  ** 先高斯去噪，在使用一阶导数获取极值（导数对噪声敏感）
  ** 梯度幅值/强度：

$ h_{x}{{(x,y)}^{2}}+h_{y}{{(x,y)}^{2}} $

** 梯度（增加最快）方向

$ \arctan (\frac{h_{y}(x,y)}{h_{x}(x,y)}) $

其中：$ h_{y}(x,y)=\frac{\partial h(x,y)}{\partial y}$， \(h(x,y)\)为二维高斯函数

• Harris 角点（corner）

** 一种显著点，在任意方向上移动一个小的观察窗，会导致大的像素变动
** 数学模型：取偏移\((u, v)\)后窗内图像变化，取\(E(u, v)\)大的patch：
\(E\left( u,v \right)=\sum\limits_{x,y}{w\left( x,y \right){{[I\left( x+u,y+v \right)-I\left( x,y \right)]}^{2}}}\)
其中，\(w(x,y)\)为窗函数，e.g., 高斯或者矩形函数

• 斑点（Blob）
  ** 拉普拉斯梯度：一阶导极值点-->二阶导数零点 ： 对噪声很敏感，先做高斯平滑
  ** 二阶高斯导数滤波（Laplacian of Gaussian, LOG）
  \({{\nabla }^{2}}\left( f\left( x,y \right)\otimes G\left( x,y \right) \right)={{\nabla }^{2}}G\left( x,y \right)\otimes G\left( x,y \right)\)
  即：先高斯滤波在拉普拉斯滤波--> 直接二阶高斯导数滤波

局部特征

• SIFT(Scale-Invariant Feature Transform)关键点
  ** 基于尺度空间的不变的特征，
  ** 具有良好的不变特性（旋转、尺度缩放、平移、亮度变化、遮挡和噪声）
  ** 独特良好，信息量丰富
  *** 适用于在海量数据库中进行快速、准确的匹配
  ** 多量性
  *** 即使少数物体也可以产生大量的SIFT特征

** 尺度空间
*** 使用不同标准差 \(\sigma\)的LOG对图片进行滤波
\({{\nabla }^{2}}L\left( x,y,\sigma \right)={{\nabla }^{2}}G\left( x,y,\sigma \right)*I\left( x,y \right)\)

*** DOG(difference of Gaussian)
**** LOG近似等于两个不同尺度\(\sigma\)的高斯差分
\(D\left( x,y,\sigma \right)=\left( G\left( x,y,k\sigma \right)-G\left( x,y,\sigma \right) \right)*I\left( x,y \right)\approx \left( k-1 \right){{\sigma }^{2}}{{\nabla }^{2}}L\left( x,y,\sigma \right)\)

** 应用
*** 计算高斯差分（LOG）尺度空间，获取极值点
*** 特征电处理
**** 位置插值
**** 去除低对比度点
**** 去除边缘点
*** 方向估计
*** 描述子提取

纹理特征

• HOG (方向梯度直方图)
  ** 梯度计算
  *** 分别计算水平和垂直梯度
  **** 梯度幅值和方向
  *** 对于彩色图片，选取梯度幅值最大的通道
  ** Block拆分

• LBP(局部二值模式)

• Gabar 滤波器组
  ** 该滤波器组类似于人类的视觉系统
  ** 频域：属于加窗傅里叶变换
  ** 空域： 一个高斯函数和正弦平面波的乘积
  \(g\left( x,y;\lambda ,\theta ,\psi ,\sigma ,\gamma \right)=\exp \left( -\frac{{{{{x}'}}^{2}}+{{\gamma }^{2}}{{{{y}'}}^{2}}}{2{{\sigma }^{2}}} \right)\exp \left( i\left( 2\pi \frac{{{x}'}}{\lambda }+\psi \right) \right)\)
  其中：\(x'=x\cos \theta + y\sin\theta\), \(y'=-x\sin \theta + y\cos\theta\)

【Tadeas】图片特征

标签：for   等于   col   识别   mit   拆分   模式   最快   函数   

原文地址：https://www.cnblogs.com/tadeas/p/11450482.html