标签:type out hit names upload bin ott scan 符号
上课的时候总会有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的D对同学上课时会交头接耳。
同学们在教室中坐成了MM行NN列,坐在第i行第j列的同学的位置是(i,j)(i,j),为了方便同学们进出,在教室中设置了KK条横向的通道,LL条纵向的通道。
于是,聪明的小雪想到了一个办法,或许可以减少上课时学生交头接耳的问题:她打算重新摆放桌椅,改变同学们桌椅间通道的位置,因为如果一条通道隔开了22个会交头接耳的同学,那么他们就不会交头接耳了。
请你帮忙给小雪编写一个程序,给出最好的通道划分方案。在该方案下,上课时交头接耳的学生的对数最少。
第一行,有55个用空格隔开的整数,分别是M,N,K,L,D(2 \le N,M \le 1000,0 \le K<M,0 \le L<N,D \le 2000)M,N,K,L,D(2≤N,M≤1000,0≤K<M,0≤L<N,D≤2000)
接下来的DD行,每行有44个用空格隔开的整数。第ii行的44个整数X_i,Y_i,P_i,Q_iXi?,Yi?,Pi?,Qi?,表示坐在位置(X_i,Y_i)(Xi?,Yi?)与(P_i,Q_i)(Pi?,Qi?)的两个同学会交头接耳(输入保证他们前后相邻或者左右相邻)。
输入数据保证最优方案的唯一性。
共两行。
第一行包含KK个整数a_1,a_2,…,a_Ka1?,a2?,…,aK?,表示第a_1a1?行和a_1+1a1?+1行之间、第a_2a2?行和a_2+1a2?+1行之间、…、第a_KaK?行和第a_K+1aK?+1行之间要开辟通道,其中a_i< a_i+1ai?<ai?+1,每两个整数之间用空格隔开(行尾没有空格)。
第二行包含LL个整数b_1,b_2,…,b_Lb1?,b2?,…,bL?,表示第b_1b1?列和b_1+1b1?+1列之间、第b_2b2?列和b_2+1b2?+1列之间、…、第b_LbL?列和第b_L+1bL?+1列之间要开辟通道,其中b_i< b_i+1bi?<bi?+1,每两个整数之间用空格隔开(列尾没有空格)。
4 5 1 2 3 4 2 4 3 2 3 3 3 2 5 2 4
2 2 4
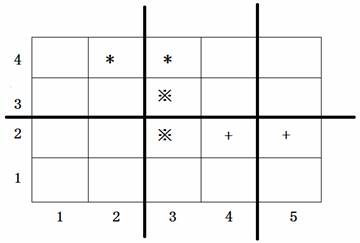
上图中用符号*、※、+标出了33对会交头接耳的学生的位置,图中33条粗线的位置表示通道,图示的通道划分方案是唯一的最佳方案。
2008年普及组第二题
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
int x[1001],y[1001],p[1001],q[1001];
int ansm[1001],ansn[1001];
int xx[1001],yy[1001];
int main(){
int m,n,k,l,d;
scanf("%d %d %d %d %d",&m,&n,&k,&l,&d);
for(int i=1;i<=d;i++){
scanf("%d %d %d %d",&x[i],&y[i],&p[i],&q[i]);
if((x[i]==p[i])){
yy[min(y[i],q[i])]++;
}
if((y[i]==q[i])){
xx[min(x[i],p[i])]++;
}
}
int maxx=-1,maxxwhere;
for(int j=1;j<=k;j++){
for(int i=1;i<=1000;i++){
if(xx[i]>maxx){
maxx=xx[i];
maxxwhere=i;
}
}
ansm[j]=maxxwhere;
xx[maxxwhere]=-1;
maxx=-1;
}
maxx=-1;
for(int j=1;j<=l;j++){
for(int i=1;i<=1000;i++){
if(yy[i]>maxx){
maxx=yy[i];
maxxwhere=i;
}
}
ansn[j]=maxxwhere;
yy[maxxwhere]=-1;
maxx=-1;
}
sort(ansm+1,ansm+1+k);
sort(ansn+1,ansn+1+l);
for(int i=1;i<=k;i++){
printf("%d ",ansm[i]);
}
printf("\n");
for(int i=1;i<=l;i++){
printf("%d ",ansn[i]);
}
printf("\n");
return 0;
}
标签:type out hit names upload bin ott scan 符号
原文地址:https://www.cnblogs.com/xiongchongwen/p/11470660.html