组成原理（数据检测的数据编码）

标签：选择   组成原理   简单   循环   bsp   注意   插入   查错   crc校验   

一、奇偶校验码：

　　一个二进制码字，如果它的码元有奇数个1，就称为具有奇性。例如，码字“10110101”有五个1，因此，这个码字具有奇性。同样，偶性码字具有偶数个1。注意奇性检测等效于所有码元的模二加，并能够由所有码元的异或运算来确定。对于一个n位字，奇性由下式给出：奇性=a0⊕a1⊕a2⊕…⊕an

　　奇偶校验只能选择一种，选择了奇校验就不能用偶校验的方式来校准了，校验位一般位于最高位。

举一个例子：

　　10 1001 奇校验 那么 它的校验位上的值应该是1，所以 编码成 1010 1001

　　如果是偶校验，就因该是 0010 1001

　　计算机通过亦或逻辑运算来检验是否符合标准

二、汉明码：

　　汉明码（Hamming Code），是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码，当计算机存储或移动数据时，可能会产生数据位错误，以侦测并更正单一比特错误。由于汉明编码简单，它们被广泛应用于内存（RAM）。

　　汉明编码检查错误、纠错能力与编码最小距离的关系是：

　　　　　　　　　　　　　　　　　　　　　　　　　　　L-1 = C+D （C <= D）（L为3）

　　n位字长的代码所需要的附加检测位数为：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　2^k  >= N+K+1

　　举例：求 0101 按偶校验配置海明码。

　　解：

　　　　n = 4；

　　　　1 　　2　　 3　　 4　　 5　　 6　　 7

　　　　C₁C₂          1      C4      0　　  0 　　0

　　Cx的值与分组有关 ，

　　　　　　　　　 C1：1，3，5，7，9，11， 13，15　　　　

　　　　　　　　　 C2：2，3，6，7，10，11，14，15

　　　　　　　　　 C3：4，5，6，7，12，13，14，15 

　　　　　　　　　 ……（自己推一下规律）

　　　　那么如何计算Cx的值呢

　　　　　　C1 =  b3 ^ b5 ^ b7 = 0;

　　　　　　C2 =  b3 ^ b6 ^ b7 = 1;

　　　　　　C3 =  b5 ^ b6 ^ b7 = 0;

　　所以生成的汉明编码为 0100101

　　　　　　如果是奇数校验那么就是：

　　　　　　C1 =  !(b3 ^ b5 ^ b7) = 1;

　　　　　　C2 =  !(b3 ^ b6 ^ b7) = 0;

　　　　　　C3 =  !(b5 ^ b6 ^ b7) = 1;

　　生成的汉明编码为 1001101

　　汉明码是具有一位验错能力的编码，那么如何验错呢？

　　例如：1101101 我随意的改了上面的汉明码，下面我们来检验一下错在哪了

　　　　P1 = !(b1 ^ b3 ^ b5 ^ b7)  = 0

　　　　P2 = !(b2 ^ b3 ^ b6 ^ b7)  = 1

　　　　P4 = !(b4 ^ b5 ^ b6) 　　 = 1

　　　　110 = 6;

　　　　第6位的确被修改了 

　　　　偶校验的类推即可。

三、循环冗余检验码(CRC)

生成多项式:G(X)=X⁴+X³+1，要求出二进制序列10110011的CRC校验码。

（1）G(X)=X⁴+X³+1,二进制比特串为11001;(有X的几次方，对应的2的几次方的位就是1)

（2）因为校验码4位，所以10110011后面再加4个0，得到101100110000，用“模2除法”(其实就是亦或^)即可得出结果；

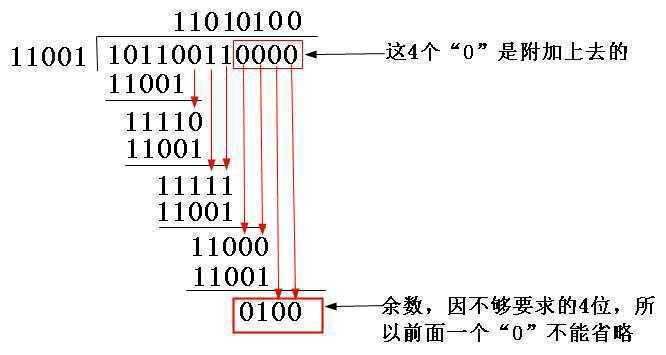
                                            图5-10 CRC校验码计算示例

 （3）CRC^101100110000得到101100110100。发送到接收端；

 （4）接收端收到101100110100后除以11001(以“模2除法”方式去除),余数为0则无差错；

　　　　至于差错，直接除以G(x)的二进制按余数查表，即可查出出错位

组成原理（数据检测的数据编码）

标签：选择   组成原理   简单   循环   bsp   注意   插入   查错   crc校验   

原文地址：https://www.cnblogs.com/daker-code/p/11477909.html