第七章-SVM支持向量机

标签：expand   one   向量   ict   解决   -o   phi   symbols   alpha   

在第二章中我们学习到感知机模型的相关知识，感知机模型是当数据线性可分时，如何利用一个超平面区分两类不同的数据。对于以上情况，支持向量机和感知机是非常相似的，两者的差别在于损失函数的不同。当线性不可分的情况下，SVM可以用核函数来实现对线性不可分的数据进行分类。

思维导图

硬间隔最大化和软间隔最大化

线性支持向量机与硬间隔最大化

所谓的硬间隔最大化，就是当选择一个超平面将两组数据进行分割开，在二维空间中，这个超平面是一条直线，每个点到该直线都会存在一个距离，使得每个点到直线的距离都比较大，因此我们选择的这个超平面就是唯一的。所有这些距离中最小的距离的点组成的平面称为支撑超平面。这些点被称为支持向量。两个支撑超平面之间的距离称为硬间隔。硬就表示硬性规定所有的点都不能在支撑超平面中间。

那么我们该如何使得间隔最大化呢？书上提到两种方式，一种是函数间隔，一种是几何间隔。最后我们选择的都是几何间隔，其中的原因又是什么呢？在此假设有一个超平面是wx+b=0，某一个实例为x0，函数间隔为|w * x0 + b|,几何间隔为|w * x0 + b|/|w|。从中可以看出，函数间隔表示的是分类预测的正确性以及确信度，如果我们成比例地改变w和b，比如改为2w和2b，此时选择的超平面没有发生改变，但是函数间隔却发生了变化，变成原来的2倍。因此，我们选择几何间隔的方式较为更好。具体过程如下：
\[ 对偶问题： \begin{array}{ll} {\displaystyle \min_{\alpha}} & {\displaystyle \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j K(x_i, x_j)-\sum_{i=1}^N \alpha_i} \\ {\text { s.t. }} & {\displaystyle \sum_{i=1}^N \alpha_i y_i=0} \\ {} & {0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N} \end{array} \\ 决策函数： f(x)=\operatorname{sign}\left(\sum_{i=1}^N \alpha_i^* y_i K(x \cdot x_i)+b^{*}\right) \\ 原始形式的最优化问题：\begin{array}{ll} \min & \displaystyle \frac{1}{2}|w|^2 + C \sum_i \xi \\ \text{ s.t. } & y_i [w \cdot \phi(x)] \geqslant 1 - \xi_i \\ & \xi_i \geqslant 0 \end{array}\\ 分离超平面为:w \cdot \phi(x) + b = 0 \]

线性支持向量机与软间隔最大化

一般情况下，训练数据集线性可分是理想的情况，但是在现实问题中，出现的都是线性不可分的情形，比如在样本中会出现噪点或者异常点，此时，硬间隔最大化是不可行的。那么，要求得太严格，又不好分类数据，该怎么办？此时，我们需要放送一些选择的标准，这也就是软间隔最大化。那么接下来的问题就是我们该如何修改硬间隔最大化，使之成为软间隔最大化，从而适应线性不可分的场景呢？如图所示：

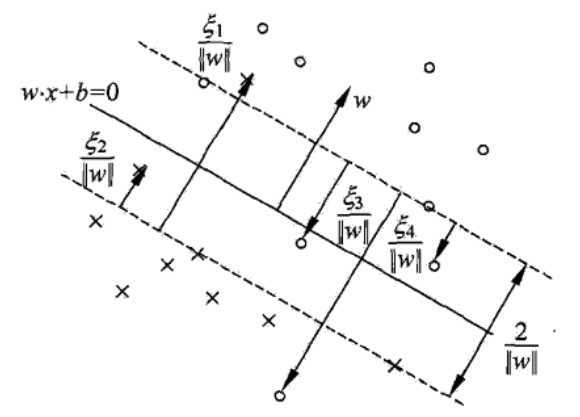
从图中可以看出，软间隔最大化其实就是允许数据点出现在两个支撑超平面之间，并且加入了惩罚项，对误分类点进行惩罚，如果偏离得越远，对误分类点的惩罚度越大。

由此可以得到最优化问题：
\[ \begin{array}{ll} {\displaystyle \min_{w, b, \xi}} & {\displaystyle \frac{1}{2}|w|^{2}+C \sum{i=1}^{N} \xi_{i}} \\ \text { s.t. } & {y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N} \\ & {\xi_{i} \geqslant 0, \quad i=1,2, \cdots, N} \end{array} \]
对偶问题：
\[ \begin{array}{ll} {\displaystyle \min_{\alpha}} & {\displaystyle \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j )+\sum_{i=1}^N \alpha_i} \\ {\text { s.t. }} & {\displaystyle \sum_{i=1}^N \alpha_i y_i=0} \\ {} & {0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N} \end{array}\最优解： w^*=\sum_{i=1}^N \alpha_i^* y_i x_i \\ b^*=y_j+\sum_{i=1}^N y_i \alpha_i^*{(x_i \cdot x_j)} \]

非线性支持向量机与核函数

从图中可以看出，右图是线性可分的情形，但是对于左图，确实线性不可分的情形。那么对于这种情形，我们可以添加核函数来解决线性不可分的问题。核函数可描述如下：
\[ k(x_i,x_j)=\phi(x_i) \cdot \phi(x_j) \]
由此可以得到以下的内容：
\[ 对偶问题： \begin{array}{ll} {\displaystyle \min_{\alpha}} & {\displaystyle \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j K(x_i, x_j)-\sum_{i=1}^N \alpha_i} \\ {\text { s.t. }} & {\displaystyle \sum_{i=1}^N \alpha_i y_i=0} \\ {} & {0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N} \end{array} \\ 决策函数： f(x)=\operatorname{sign}\left(\sum_{i=1}^N \alpha_i^* y_i K(x \cdot x_i)+b^{*}\right) \原始形式的最优化问题：\begin{array}{ll} \min & \displaystyle \frac{1}{2}|w|^2 + C \sum_i \xi \\ \text{ s.t. } & y_i [w \cdot \phi(x)] \geqslant 1 - \xi_i \\ & \xi_i \geqslant 0 \end{array}\分离超平面为:w \cdot \phi(x) + b = 0 \]
对于这种情形，也存在一些缺点，就是当对于一个实际问题时，我们不知道该用什么样的曲面更好地分离数据，选择一个合适的核函数存在一个挑战，这就需要我们面对实际场景问题进行实际分析了。

相关的数学推导和例题计算

1.线性支持向量机还可以定义以下形式：
\[ \begin{array}{ll} \min & \displaystyle(\frac{1}{2}||w||^2+C\sum_{i=1}^N\xi_i^2)\\\displaystyle \text{ s.t. } & y_i(wx_i+b) \geq 1- \xi_i \\ \text{ s.t. } & \xi_i \geq 0 \end{array} \]
求其对偶形式。

求解过程：

第一步：原始问题如问题可知，确定拉格朗日函数。
\[ 假设\alpha和\mu是拉格朗日乘子，则拉格朗日函数为：\\begin{array}{ll} L(w,b,\xi_i,\alpha_i,\mu_i)=\frac{1}{2}||w||^2+C\sum_{i=1}^N\xi_i^2-\sum_{i=1}^2\alpha_i[y_i(wx_i+b)-1+\xi_i]-\sum_{i=1}^2\mu_i\xi_i \\text{ s.t. } \ {} \alpha_i \geq 0,\mu_i \geq 0 & \displaystyle (1) \end{array}\因此转化成：\begin{array}{ll} \max_{\alpha,\mu} \min_{w,b,\xi_i} & \displaystyle L(w,b,\xi_i,\alpha_i,\mu_i) \end{array} \]
第二步：确定对偶形式，通过求偏导找出对偶形式对拉格朗日乘子的极大。
\[ \nabla_w L(w,b,\xi_i,\alpha_i,\mu_i) = w - \sum_{i=1}^N\alpha_iy_ix_i=0 \\nabla_b L(w,b,\xi_i,\alpha_i,\mu_i) = - \sum_{i=1}^N\alpha_iy_i=0 \\nabla_{\xi_i} L(w,b,\xi_i,\alpha_i,\mu_i) = 2C\xi_i - y_ix_i - \mu_i=0 \\rightarrow \ =\left\{\begin{aligned} w=\sum_{i=1}^N\alpha_iy_ix_i & & (2) \\sum_{i=1}^Ny_ix_i=0 & & (3) \2C\xi_i - y_ix_i - \mu_i=0 & & (4) \end{aligned} \right. 将(2)-(4)代入L(w,b,\xi_i,\alpha_i,\mu_i)中可得:\\min_{\alpha,\mu}L(\alpha,\mu)=\frac{1}{2}\sum_{i=1}^N\alpha_iy_ix_i \cdot \sum_{i=1}^N\alpha_iy_ix_i - \sum_{i=1}^Ny_ix_ib +C \cdot \sum_{i=1}^N\frac{(\alpha+\mu)^2}{4C^2}+\sum_{i=1}^N\alpha_i-\sum_{i=1}^N\alpha_i\xi_i-\sum_{i=1}^N\mu_i\xi_i\= -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_ix_j) + \sum_{i=1}^N\frac{(\alpha+\mu)^2}{4C^2} + \sum_{i=1}^N\alpha_i-\sum_{i=1}^N\alpha_i\frac{\alpha+\mu_i}{2C}-\sum_{i=1}^N\mu_i\frac{\alpha+\mu_i}{2C}\= -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_ix_j) + \sum_{i=1}^N\alpha_i - \sum_{i=1}^N\frac{(\alpha+\mu)^2}{4C^2}\s.t. \ \alpha_i* \geq 0\s.t. \ \mu_i* \geq 0 \]
第三步：根据KKT条件可确定结果。
\[ \left\{\begin{aligned} \alpha_i^*[y_i(w^*x_i+b^*)-1+\xi_i^*]=0 \\mu_i^*\xi_i^*=0 \\xi_i^* \geq 0 \\alpha_i^* \geq 0\\mu_i^* \geq 0 \end{aligned} \right.\=又因\left\{\begin{aligned} \alpha_i^* > 0\\mu_i^* > 0 \end{aligned} \right.\\therefore =>\left\{\begin{aligned} \alpha_i^*[y_i(w^*x_i+b^*)-1+\xi_i^*]=0\\mu_i^* = 0 \end{aligned} \right. \\therefore => \left\{\begin{aligned} \alpha_i^*[y_i(w^*x_i+b^*)-1]=0\y_i=w^*x_i+b^* \\ b^*= y_i-w^*x_i^* \end{aligned} \right. \]

\[ 2.已知数据集D中，正实例点(Y=1)是x_1=(1,2)^T,x_2=(2,3)^T,x_3=(3,3)^T,\\负实例点是x_4=(2,1)^T,x_5=(3,2)^T。\试求最大间隔分类超平面和分类决策函数。 \]

解：根据实例点，分析可知，该数据集是线性可分的。

第一步：确定原始问题形式和对偶形式。
\[ 原始问题：\\ \min_{w,b} \frac{1}{2}||w||^2 \\ s.t. \ y_i(wx_i+b)-1 \geq 0,i=1,2,3,4,5\\ 对偶问题：\\ L(\alpha)=\min_\alpha \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_ix_j) + \sum_{i=1}^N\alpha_i\\ s.t. \ \alpha_i* \geq 0,i=1,2,3,4,5\\]
第二步：由上式可代入实例点计算。
\[ \left\{\begin{aligned} L(\alpha)= \frac{1}{2}\alpha_1\alpha_1y_1y_1(x_1 \cdot x_1)+\frac{1}{2}\alpha_1\alpha_2y_1y_2(x_1 \cdot x_2) +\frac{1}{2}\alpha_3\alpha_1y_3y_1(x_1 \cdot x_3) \\+ \frac{1}{2}\alpha_1\alpha_4y_1y_4(x_1 \cdot x_4)+\frac{1}{2}\alpha_1\alpha_5y_1y_5(x_1 \cdot x_5)\\+\frac{1}{2}\alpha_2\alpha_1y_2y_1(x_2 \cdot x_1)+\frac{1}{2}\alpha_2\alpha_2y_1y_2(x_2 \cdot x_2) +\frac{1}{2}\alpha_2\alpha_3y_2y_3(x_2 \cdot x_3) \\+ \frac{1}{2}\alpha_2\alpha_4y_2y_4(x_2 \cdot x_4)+\frac{1}{2}\alpha_2\alpha_5y_2y_5(x_2 \cdot x_5)+\\...\\ +\frac{1}{2}\alpha_5\alpha_1y_5y_1(x_5 \cdot x_1)+\frac{1}{2}\alpha_5\alpha_2y_5y_2(x_5 \cdot x_2) +\frac{1}{2}\alpha_5\alpha_1y_5y_1(x_5 \cdot x_3) \\+ \frac{1}{2}\alpha_5\alpha_4y_5y_4(x_5 \cdot x_4)+\frac{1}{2}\alpha_5\alpha_5y_5y_5(x_5 \cdot x_5)\\ = \frac{5}{2}\alpha_1+\frac{13}{2}\alpha_2^2+9\alpha_3^2+\frac{5}{2}\alpha_4^2+\frac{13}{2}\alpha_5^2\\+8\alpha_1\alpha_2+9\alpha_2\alpha_3-4\alpha1_1\alpha_4-7\alpha_1\alpha_5\\+15\alpha_2\alpha_3-7\alpha_2\alpha_4-12\alpha_2\alpha_5\\-9\alpha_3\alpha_4-15\alpha_3\alpha_5+8\alpha_4\alpha_5\\-\alpha_1-\alpha_2-\alpha_3-\alpha_4-\alpha_5 \ ..........(1)\\ \alpha_1y_1+\alpha_2y_2+\alpha_3y_3+\alpha_4y_4+\alpha_5y_5=0\ ..........(2) \end{aligned} \right.\\]
第二步：求偏导。
\[ 联立上述(1)(2)并分别对：\\ \nabla_{\alpha_1}L(\alpha)=5\alpha_1+13(\alpha_1+\alpha_2+\alpha_3-\alpha_4-\alpha_5)+8\alpha_2+9\alpha_3-4\alpha_4\\-14\alpha_1-7(\alpha_2+\alpha_3-\alpha_4)-12\alpha_2-15\alpha_3+8\alpha_4-2=0 \\ =>4\alpha_1+2\alpha_2-2\alpha_4-2=0...........................(1)\\ \nabla_{\alpha_2}L(\alpha)=2\alpha_1+2\alpha_2+\alpha_3-2=0.........................................(2)\\ \nabla_{\alpha_3}L(\alpha)=2\alpha_2+\alpha_3+\alpha_4-2=0.........................................(3)\\ \nabla_{\alpha_4}L(\alpha)=-2\alpha_1+\alpha_3+2\alpha_4=0.........................................(4)\\ \rightarrow \ =\left\{\begin{aligned} 4\alpha_11+2\alpha_2-2\alpha_4-2=0 \\ 2\alpha_1+2\alpha_2+\alpha_3-2=0 \\ 2\alpha_2+\alpha_3+\alpha_4-2=0\\ -2\alpha_1+\alpha_3+2\alpha_4=0 \end{aligned} \right.\\]
第三步：根据KKT条件求解。
\[ 首先比较容易求解出\alpha_2=0。\\ \rightarrow \ =\left\{\begin{aligned} 2\alpha_1-\alpha_4-1=0 \\ \alpha_3+\alpha_4-2=0 \\ 2\alpha_2+\alpha_3+\alpha_4-2=0\\ -2\alpha_1+\alpha_3+2\alpha_4=0 \end{aligned} \right.\\ 因此可得到:\\ \begin{array}{ll} {\displaystyle ①\left\{\begin{aligned} \alpha_2=0 \\ \alpha_1=0 \end{aligned} \right.} & {\displaystyle ②\left\{\begin{aligned} \alpha_2=0 \\ \alpha_3=0 \end{aligned} \right.} & {\displaystyle ③\left\{\begin{aligned} \alpha_2=0 \\ \alpha_1=0 \end{aligned} \right.}\end{array}\\ 当①计算出\alpha_4=-2,不符合条件，因此舍去。\\ 因此可以使用边界最小值可求得:\\ \begin{array}{ll} {\displaystyle ①\left\{\begin{aligned} \alpha_1=\alpha_2=\alpha_4=0 \\ \alpha_3=\alpha_5=2 \end{aligned} \right.} & {\displaystyle ②\left\{\begin{aligned} \alpha_2=\alpha_3=\alpha_5=0 \\ \alpha_1=\alpha_4=1 \end{aligned} \right.} & {\displaystyle ③\left\{\begin{aligned} \alpha_2=\alpha_4=0 \\ \alpha_1=\frac{1}{2}\\ \alpha_3=2\\ \alpha_5=\frac{5}{2} \end{aligned} \right.}\end{array}\\ \rightarrow \ \begin{array}{ll} {\displaystyle ①可得：L_1=-2}\\ {\displaystyle ②可得：L_1=-1}\\ {\displaystyle ③可得：L_1=-\frac{5}{2}} \end{array}\\ 因此，L最小为-\frac{5}{2}，此时\alpha^*=(\frac{1}{2},0,3,0,\frac{5}{2}).\\ \therefore w^*=\sum_{i=1}^N\alpha^*y_ix_i=(-1,2)\\ \therefore \alpha_1=\frac{1}{2},b^*=y_i-w^* \cdot x_i=-2\\ \therefore \left\{\begin{aligned} 分离超平面为：-x^{(1)}+2x^{(2)}-2=0 \\ 间隔边界正实例为：-x^{(1)}+2x^{(2)}-2=1\\ 间隔边界负实例为：-x^{(1)}+2x^{(2)}-2=-1 \end{aligned} \right. \]

序列最小化最优化算法（Sequential Minimal Optimization-SMO）

\[ 对偶问题：\begin{array}{ll} {\displaystyle \min *{\alpha}} & {\displaystyle \frac{1}{2} \sum*{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j K(x_i, x_j)-\sum_{i=1}^N \alpha_i} \\ {\text { s.t. }} & {\displaystyle \sum_{i=1}^N \alpha_i y_i=0} \\ & {0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N} \end{array} \\ 需要优化的变量是\alpha_i有N个，当数据量很大的时候，需要优化的变量非常多，很难计算，\\所以不优化所有的变量，每一次优化其中的一部分变量。在该算法中，每次优化两个变量。 \]

Python代码实现

利用编程实现：

\[ 已知数据集D中，正实例点(Y=1)是x_1=(1,2)^T,x_2=(2,3)^T,x_3=(3,3)^T,\\负实例点是x_4=(2,1)^T,x_5=(3,2)^T。 \]

自编程实现

"""构造L(a,b,c,d)表达式,e=a+b+c-d"""


def creat(co, X, y, a, b, c, d, e):
    L_0 = co * X * y
    L_1 = L_0.sum(axis=0)
    L = np.dot(L_1, L_1) / 2 - co.sum()
    # 将e=a+b+c-d代入，化简整理
    L = expand(L.subs(e, a + b + c - d))
    return L


"""若L无解，则从L的多个边界求解"""


def _find_submin(L, num):
    if num.shape[0] == 1:
        return None
    else:
        res = []
        for i in range(num.shape[0]):
            L_child = L.subs({num[i]: 0})
            num_child = np.delete(num, i, axis=0)
            res.append(_find_min(L_child, num_child))
        return res


"""判断方程是否有唯一不小于0且不全为0的实数解"""


def _judge(res):
    for s in res.values():
        try:
            if float(s) < 0:
                return False
        except:
            return False
    return True if sum(res.values()) != 0 else False


"""求解所有可能的极值点，若极值不存在或不在可行域内取到，则在边界寻找极值点"""


def _find_min(L, num):
    pro_res = []
    res = solve(diff(L, num), list(num))
    # 方程有解
    if res:
        # 方程有唯一不小于0且不全为0的实数解
        if _judge(res):
            pro_res.append(res)
            return pro_res
        # 方程有无数组解，到子边界寻找极值点
        else:
            value = _find_submin(L, num)
            pro_res.append(value)
    # 方程无解，到子边界寻找极值点
    else:
        value = _find_submin(L, num)
        pro_res.append(value)
    return pro_res


"""将所有结果排列整齐"""


def reset(res):
    if not isinstance(res[0], list):
        if res[0]:
            res_list.append(res[0])
    else:
        for i in res:
            reset(i)


"""求解极小值点"""


def find_min(L, num, a, b, c, d, e):
    # 求解所有可能的极小值点
    results = _find_min(L, num)
    reset(results)
    L_min = float("inf")
    res = None
    # 在所有边界最小值中选取使得L(a,b,c,d)最小的点
    for i in res_list:
        d_i = dict()
        for j in [a, b, c, d]:
            d_i[j] = i.get(j, 0)
        result = L.subs(d_i)
        if result < L_min:
            L_min = result
            res = d_i
    # 将e 计算出来并添加到res中
    res[e] = res[a] + res[b] + res[c] - res[d]
    return res


"""计算 w b"""


def calculate_w_b(X, y, res):
    alpha = np.array([[i] for i in res.values()])
    w = (alpha * X * y).sum(axis=0)
    for i in range(alpha.shape[0]):
        if alpha[i]:
            b = y[i] - w.dot(X[i])
            break
    return w, b


"""绘制样本点、分离超平面和间隔边界"""


def draw(X, y, w, b):
    y = np.array([y[i][0] for i in range(y.shape[0])])
    X_po = X[np.where(y == 1)]
    X_ne = X[np.where(y == -1)]
    x_1 = X_po[:, 0]
    y_1 = X_po[:, 1]
    x_2 = X_ne[:, 0]
    y_2 = X_ne[:, 1]
    plt.plot(x_1, y_1, "ro")
    plt.plot(x_2, y_2, "gx")
    x = np.array([0, 3])
    y = (-b - w[0] * x) / w[1]
    y_po = (1 - b - w[0] * x) / w[1]
    y_ne = (-1 - b - w[0] * x) / w[1]
    plt.plot(x, y, "r-")
    plt.plot(x, y_po, "b-")
    plt.plot(x, y_ne, "b-")
    plt.show()


def main():
    # 构建目标函数L(a,b,c,d,e)
    a, b, c, d, e = symbols("a,b,c,d,e")
    X = np.array([[1, 2],
                  [2, 3],
                  [3, 3],
                  [2, 1],
                  [3, 2]])
    y = np.array([[1], [1], [1], [-1], [-1]])
    co = np.array([[a], [b], [c], [d], [e]])
    L = creat(co, X, y, a, b, c, d, e)
    num = np.array([a, b, c, d])
    # 求解极小值点
    global res_list
    res_list = []
    res = find_min(L, num, a, b, c, d, e)
    # 求w b
    w, b = calculate_w_b(X, y, res)
    print("w", w)
    print("b", b)
    # 绘制样本点、分离超平面和间隔边界
    draw(X, y, w, b)

SKlearn库实现

def draw(X,y,w,b):
    y=np.array([y[i] for i in range(y.shape[0])])
    X_po=X[np.where(y==1)]
    X_ne=X[np.where(y==-1)]
    x_1=X_po[:,0]
    y_1=X_po[:,1]
    x_2=X_ne[:,0]
    y_2=X_ne[:,1]
    plt.plot(x_1,y_1,"ro")
    plt.plot(x_2,y_2,"gx")
    x=np.array([0,3])
    y=(-b-w[0]*x)/w[1]
    y_po=(1-b-w[0]*x)/w[1]
    y_ne=(-1-b-w[0]*x)/w[1]
    plt.plot(x,y,"r-")
    plt.plot(x,y_po,"b-")
    plt.plot(x,y_ne,"b-")
    plt.savefig('svm.jpg')
    plt.show()

def main():
    X=np.array([[1,2],
                [2,3],
                [3,3],
                [2,1],
                [3,2]])
    y=np.array([1,1,1,-1,-1])
    clf=SVC(C=0.5,kernel="linear")
    clf.fit(X,y)
    w=clf.coef_[0]
    b=clf.intercept_
    print(clf.support_vectors_)
    print(w,b)
    print(clf.predict([[5,6],[-1,-1]]))
    print(clf.score(X,y))
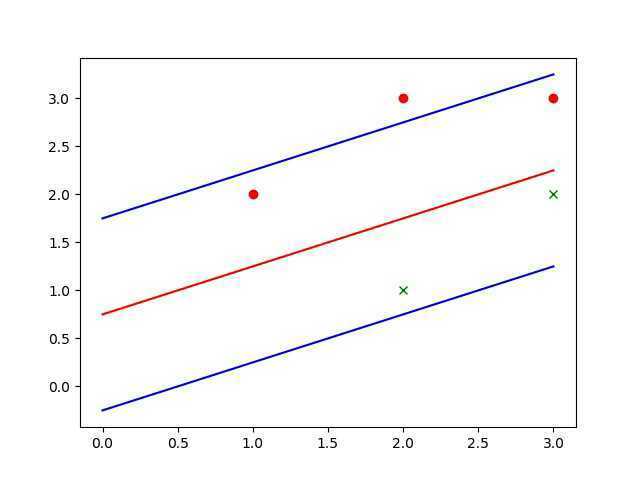
    draw(X,y,w,b)

实现结果：

第七章-SVM支持向量机

标签：expand   one   向量   ict   解决   -o   phi   symbols   alpha   

原文地址：https://www.cnblogs.com/cecilia-2019/p/11483264.html