标签：src   二叉查找树   nod   二叉树   于平   这一   sentinel   假设   定义   

红黑树及其基本操作

红黑树的定义

? 红黑树是一种自平衡二叉查找树。它相比于平衡二叉树的优点在于，其的特性可以让其在任何条件下保持树的高度小于等于log n，所以其即使在最坏条件下对于增删查改这样的基本操作也能保持O(log n)的时间复杂度；另外，相比于严格平衡的AVL树，红黑树是一种不严格的平衡二叉树，这样就减少了在实际使用过程中为了保持树的平衡性而在增删节点时不断进行的平衡化操作，效率更高。这些特性使得它得到了相比平衡二叉树更加广泛的应用，例如C++的STL中的map、set以及Java中的TreeMap都是利用它实现的

红黑树有五条性质：

1. 每一个节点要么是红色，要么是黑色

2. 根节点是黑色的

3. 每个终节点是黑色的

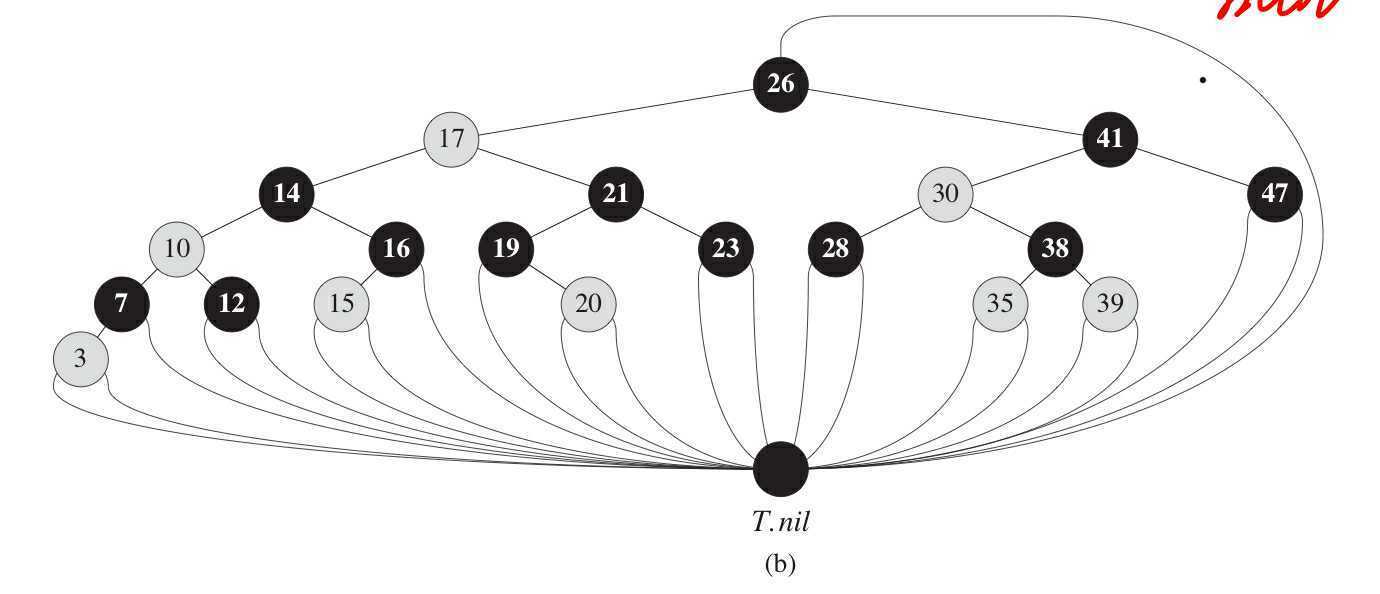
   注意，这里的终节点和我们平常理解的叶子节点是不一样的。《Algorithms》中用sentinel node来表示，它指的是我们所说的叶子节点的子节点，其parent、left、right属性值都是null。很显然，它也是需要实例化的，为了节省不必要的开销，书中将所有的终节点指针都指向同一个对象，当然这样就没有办法用该节点的parent属性了

   

4. 如果一个节点是红色的，则它的两个孩子节点一定是黑色的

5. 对于每一个节点，从该节点到终节点的每一条路径上有相同数量的黑色节点

证明：有n个非终节点的红黑树的高度最高为2log(n+1)

引理：以节点x为根的子树包括至少2^(bh(x))-1个非终节点。其中bh(x)叫黑色高度，指的是从这个点（不包括该点）到终结点（包括终结点）的黑色点个数

证明引理：使用数学归纳法

1. 如果子树x的高度为0，则也就是说这个子树只有x这一个节点，所以内部有2^(0)-1=0个非终节点。

2. 如果子树高度不为0。由于其为黑色节点（为什么一定是黑色节点？因为红黑树的根必须是黑色的），其子节点可以说红色，也可以是黑色，所以对于其两个子节点来说，黑色高度可能是bh(x)[子节点为红色的情况],也可能是bh(x)-1[子节点为黑色的情况，也是能构成子树的情况，下面讨论的就是这种]。如果假设该引理正确，则对于其子节点来说，由其为根的子树至少有2^(bh(x)-1)-1个非终节点，那么对于节点x，其非终结点数量就是2*2^(bh(x)-1)-2+1=2^(bh(x))-1。（注意最后加的那个1是节点x自己）

3. 引理得证

证明原命题

由于性质4，从根节点到终结点的每一条路径上，至少有一半的节点是黑色的（因为出现红色节点必须跟着一对黑色子节点，而黑色节点则是没有要求的），所以我们假设一棵树高度为h，那么这样的一条支路上至少有h/2个黑色节点，也就是说这棵树的黑色高度至少为h/2，由引理可知，该树至少有2^(h/2)-1个非终节点，方程化简一下就能得到命题结果。

**由这个命题我们可以看出来，节点的高度一定是log级别的，那么由于其是有序的，在增删查改时采用的是二叉搜索树通用的方法，所以遍历的高度不会高于树的高度，这就是红黑树能保持O(logn)的原因。

红黑树的插入

红黑树的删除

--

Reference

红黑树及其基本操作

标签：src   二叉查找树   nod   二叉树   于平   这一   sentinel   假设   定义   

原文地址：https://www.cnblogs.com/jiading/p/11508828.html