标签:描述 png 根据 一点 pre 思路 fine namespace 链接
复习dp(迪皮)的时候刷到了一道简单路径压缩的题目(一点不会qwq)
正解:
首先呢,我们看到题目,自然而然的会想到这种思路:
设状态变量dp[i]表示从第一个格子开始经过一些跳跃跳到第i个格子上所踩到的最小石子数目。
那么,根据每一次跳s~t个格子,我们可以得出dp[i]可以从dp[i-t]到dp[i-s]转移过来,要综合考虑的话呢,就要在所有之前的情况中取一个石子数最小的在加上当前位置是否有石子数,就是dp[i]的值。
于是呢,有了整体思路,我们开始敲起了代码。
浏览数组范围时发现了这样一个东西:
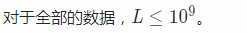 awsl
awsl
这空间时间都会炸吧。。。
于是乎,我们上述的简单套路就被ban掉了。
开始思考:

我们发现在这种数据下,石子间的间隔变得非常的大。
能不能压缩一下那些多余的路径,但是却对答案没有影响呢?
首先,摘取洛谷题解中一位dalao的做法:


我直接没看,被ex到了。
自己思考:
看了看数据范围:
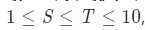
观察dp式子dp[i]=max(dp[i-t]~dp[i-s])+flag[i];flag[i]表示第i个位置有没有石子。
当一段区间不存在石子时,flag就无用了。
于是说白了,就是个统计最大值的过程一旦统计完dp[i]到dp[i-t]的最大值,其后面flag等于0的情况直接就可以跳过了。
不难想出,统计dp[i]到dp[i-t]这个区间的最大值一共需要lcm(s,t)次。
感性理解。。。
于是我们得出了最短压缩长度90.。?(90=9*10,10,10的情况直接特判就行了)
那么,把多余90的距离都压缩成90一定能保证结果不变。
上代码:
#include<cstdio> #include<cstring> #include<algorithm> #define maxn 214748364 using namespace std; int read() { int ans=0; char ch=getchar(),last=‘ ‘; while(ch>‘9‘||ch<‘0‘)last=ch,ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘)ans=(ans<<3)+(ans<<1)+ch-‘0‘,ch=getchar(); return last==‘-‘?-ans:ans; } int min(int a,int b){return a<b?a:b;} inline bool cmp(int a,int b) {return a<b;} int l,s,t,m,sz[20003],ans,dis[20003],sum,flag[20001],dp[20001]; int main(){ l=read(); s=read(),t=read(),m=read(); if(s==t) { int bol; for(int i=1;i<=m;i++) { bol=read();ans+=((bol%s)==0); } printf("%d\n",ans);return 0; } for(int i=1;i<=m;i++) sz[i]=read(); sort(sz+1,sz+1+m,cmp); for(int i=1;i<=m;i++) dis[i]=min(sz[i]-sz[i-1],90);//dis[i]表示第i个石子到第i-1个石子的距离差 dis[m+1]=min(l-sz[m],100); for(int i=1;i<=m;i++) sum+=dis[i],flag[sum]=1; sum+=dis[m+1]; for(int i=1;i<=sum+9;i++) { dp[i]=maxn; for(int j=s;j<=t;j++) { if(i>=j)dp[i]=min(dp[i],dp[i-j]+flag[i]); } } int minn=maxn; for(int i=sum;i<=sum+9;i++) { minn=min(minn,dp[i]); } printf("%d",minn); return 0; }
完结/
也就是说,对于s=t=10的极端情况,只要看100的倍数上有没有石子统计一下就行了。
对于次大的情况s=9,t=10,时,只要把s
标签:描述 png 根据 一点 pre 思路 fine namespace 链接
原文地址:https://www.cnblogs.com/lbssxz/p/11512697.html