标签:while 二分 idt print $1 原来 次数 max 结果
题意:
给定一个长度为 $n$ 的序列,并得到了 $k$ 次操作的机会,每一次操作就是把其中一个数的值加 $1$。
求合理安排这 $k$ 次操作,使得结果序列的中位数最大。
$1 \le n \le 2*10^5,1 \le k \le 10^9$
分析:
我们可以用贪心策略想,如果给原始序列小于中位数的数进行操作,那么答案肯定不是最优的,不如给较大的数字。
所以,我们可以删去这个序列中所有小于中位数的数。
删去之后,那原来的中位数就变成了这个序列中最小的数了。
问题便转换成 “最小值最大” 这一类问题了,没错,可以二分答案。
我们肯定要尽可能地给最小的数进行操作,但是这个数一旦超越了其它数就不再是最小的数了。
所以,我们要分析一下,以下图为例:
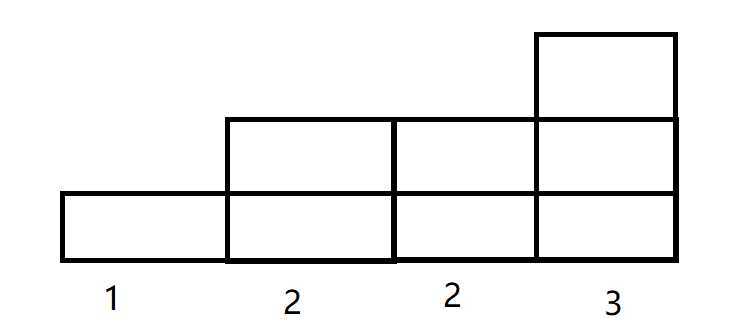
我们要让 $1$ 号点尽量大,那么就要多分给一号点操作次数,但同时要保证 $1$ 号均不大于其它的数。
所以,我们将高度(即答案)进行二分:
如果要让 $1$ 号点填充到两层,那么要这么做:
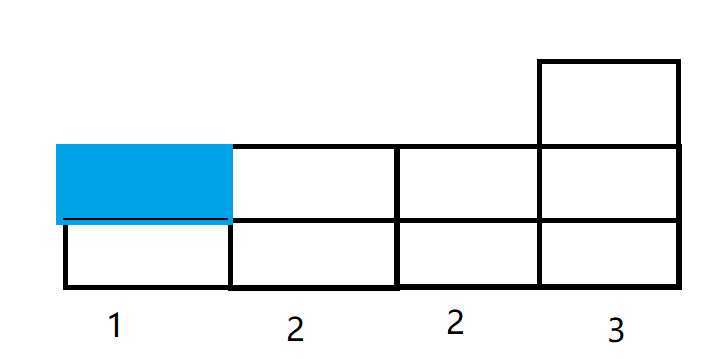
这样需要进行 $1$ 次操作;
如果要让 $1$ 号点填充到三层,要这样:
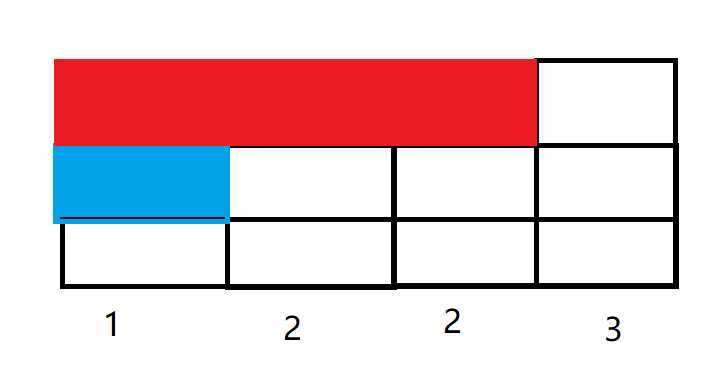
一共需要 $1+3=4$ 次操作。
所以,检验条件就是看看所有小于待定高度的点高度差加起来是否会超过 $k.$
这样,就可以写代码了:
#include <algorithm> #include <cstdio> typedef long long ll; ll n, k, a[200010], ans, l, r; bool check(ll x){ ll sum = 0; for(ll i=1; i<=n; i++) if(a[i] < x) sum += x - a[i]; //算高度差之和 else break; return sum <= k; //检验条件 } int main(){ scanf("%lld%lld", &n, &k); for(ll i=1; i<=n; i++) scanf("%lld", &a[i]); std::sort(a + 1, a + n + 1); //注意二分的单调性,因此要排序 n = n / 2 + 1; //为方便,这里提前改变 n 的规模 for(ll i=1; i<=n; i++) a[i] = a[n + i - 1]; l = 1, r = 2e9; while(l < r){ ll mid = (l + r + 1) >> 1; if(check(mid)) l = mid; else r = mid - 1; } printf("%lld\n", l); return 0; }
复杂度 $\text{O(n log n)}.$
另外,这题还有别的做法,如贪心(复杂度线性)等,此处不说明了,有兴趣的可以去研究一下。
标签:while 二分 idt print $1 原来 次数 max 结果
原文地址:https://www.cnblogs.com/zengpeichen/p/11515613.html