标签：style blog http color strong sp div on 2014
????设实对称矩阵
????
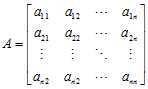
方阵
的行列式用
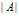表示，其各阶顺序主子式为
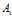，则
????一阶顺序主子式：
????
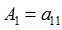
二阶顺序主子式：
????
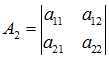
三阶顺序主子式：
????
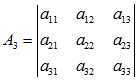
其余各阶顺序主子式依次类推。下表给出各矩阵的定义以及充分必要条件
名称 | 定义 | 充要条件 | ||
正定矩阵 | 特征值都大于零的实对称矩阵 | 所有各阶顺序主子式都大于零，即 | ||
半正定矩阵 | 特征值都不小于零的实对称矩阵 |
| ||
负定矩阵 | 特征值都小于零的实对称矩阵 | ???? | ||
半负定矩阵 | 特征值都不大于零的实对称矩阵 |
| ||
不定矩阵 | 特征值既有大于零又有小于零的实对称矩阵 | 有两个奇数阶顺序主子式，其中一个为正，一个为负 | ||
标签：style blog http color strong sp div on 2014
原文地址：http://www.cnblogs.com/shiguihong/p/4052969.html
