红黑树

标签：定义   http   长度   大整数   顺序   二叉搜索树   ack   sub   等等   

它是为了解决二叉查找树的查找时间复杂度最差是O(n)的问题而发明的数据结构算法。

BST的查找运行时间和BST的高度有关。一个树的高度指的是从树的根开始所能到达的最长的路径长度。

因为二叉搜索树的结构可能是一个链表，在这种情况下，在 BST 中查找节点与在数组（Array）中查找就基本类似了。

如这个例子：

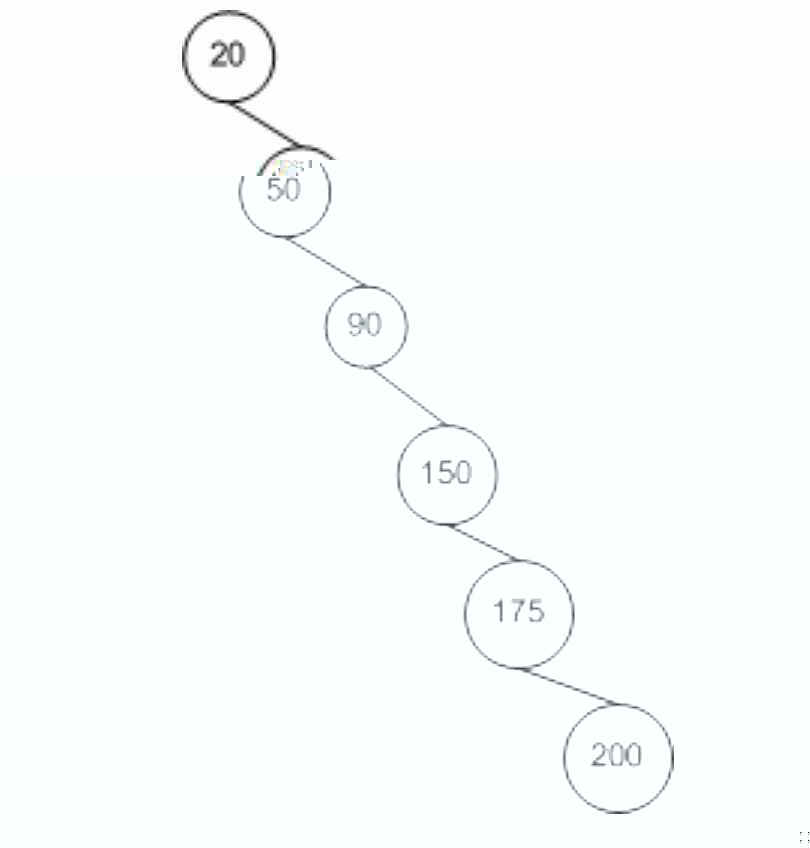
有6个节点，它的时间复杂度是O(n)。假如要查找节点200，那么节点会比较5此，相当于遍历所有节点了。

这太浪费时间了，因此降低树的高度，就可以减少时间复杂度。

我们知道二叉搜索树的搜索节点的最小时间复杂度是 O(log­₂n)。因此找到一个高度和节点数量的最佳比例。让它的时间复杂度维持在O(log­₂n)。

期望是：

如果树中节点的数量为 n，则一棵满足O(log₂n) 渐进运行时间的 BST 树的高度应接近于比 log₂n 小的最大整数。

但实际问题是：

如何保证 BST 的拓扑结构始终保持树高度与节点数量的最佳比例？

因为 BST 的拓扑结构与节点的插入顺序息息相关，一种方式是通过数据的乱序来保证。所以必须在插入节点前就得到数据。

但是如果无法掌控数据的来源，怎么做？一种方案是新的节点插入不会打乱BST树的平衡。这种始终维持树的平衡状态的数据结构称为：自平衡二叉查找树。self-balancing binary search tree.

一棵平衡树指的是树能够保持其高度与广度能够保持预先定义的比例。有许多种不同的自平衡 BST 数据结构，例如 AVL 树、红黑树（Red-Black Tree）、2-3 树、2-3-4 树、伸展树（Splay Tree）、B 树等等。

本文讲解：红黑树。

红黑树

算法导论对R-B Tree的介绍：
红黑树，一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。

通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树

标签：定义   http   长度   大整数   顺序   二叉搜索树   ack   sub   等等   

原文地址：https://www.cnblogs.com/chentianwei/p/11517545.html