标签:误差 工作 loss 小技巧 总结 优化 权重 特性 原因
本节涉及的知识点:
1.在程序中查看变量的取值
2.张量
3.用张量重新组织输入数据
4.简化的神经网络模型
5.标量、多维数组
6.在TensorFlow中查看和设定张量的形态
7.用softmax函数规范可变参数
8.小结:线性问题
x = 1 y = 2.2 z = "adc" print("x is: %d" % x) print("y is: %f" % y) print("z is: %s" % z)
x is: 1 y is: 2.200000 z is: adc
import tensorflow as tf x1 = tf.placeholder(dtype=tf.float32) x2 = tf.placeholder(dtype=tf.float32) x3 = tf.placeholder(dtype=tf.float32) print("x1: %s" % x1) yTrain = tf.placeholder(dtype=tf.float32) w1 = tf.Variable(0.1,dtype=tf.float32) w2 = tf.Variable(0.1,dtype=tf.float32) w3 = tf.Variable(0.1,dtype=tf.float32) print("w1: %s" % w1) n1 = x1 * w1 n2 = x2 * w2 n3 = x3 * w3 print("n1: %s" % n1) y = n1 + n2 + n3 print("y: %s" % y)
x1: Tensor("Placeholder:0", dtype=float32)
w1: <tf.Variable ‘Variable:0‘ shape=() dtype=float32_ref>
n1: Tensor("mul:0", dtype=float32)
y: Tensor("add_1:0", dtype=float32)
其中,x1是一个Tensor对象,由操作“Placeholder:0”这个操作而来,这个操作就是定义x1 时
x1 = tf.placeholder(dtype=tf.float32)
语句中的tf.placeholder函数,是定位符的一个操作。后面的数字代表该操作输出结果的编号。【一个编号可能会有多个输出结果】,“0”代表第一个输出结果的编号,大多数操作也只有一个输出结果。
w1是一个tf.Variable对象,也就是可变参数对象
n1 是一个Tensor 对象,由操作 "mul:0"得来。mul 是 乘法multiply 操作的简称,对应于定义n1时的语句 —— n1 = x1 *w1
y 是一个Tensor对象,由操作 “add_1:0” 得来,对应于定义y时的语句 y = n1 + n2 + n3【下划线和数字1的原因是TensorFlow会把这个算式的两个加号拆成类似于n1 + (n2 + n3) 这样的两个加法操作,所以加序号以区分】
上一节神经网络模型图中的所有节点,包括输入层、隐藏层、输出层 的节点,都对传入自身的数据进行一定的计算操作并输出数据。
节点对应的计算操作在程序中是用运算符来体现的,而输出的数据在程序中体现为 Tensor 【张量】类型的一个对象,
# 虽然张量只是代表模型图中某个节点的输出数据,但在程序中,一般用这个节点的名称来命名这个节点输出的张量
类似Tensor("mul:0",dtype=float32) 这样一个张量的输出信息中,括号的第一部分就是它对应的操作,第二部分对应它的输出数据类型。如果张量是由多个操作计算而来,输出信息中的操作将是其中的最后一个

在之前设计的神经网络中,总共有3个分数,如果再要加一个分数项,需要改变整个网络模型。所以在通常的神经网络中,很多时候会把这一串的数据组织成一个“向量“ 来送入神经网络进行计算。
把输入数据改为张量的形式:
import tensorflow as tf x = tf.placeholder(shape=[3], dtype=tf.float32) #命名参数shape,这是表示变量x的形态的,[3]表示输入占位符x的数据将是一个含有3个数字的数组,也就是一个三维张量 yTrain = tf.placeholder(shape=[], dtype=tf.float32) #yTrain 是一个普通数字,不是张量,如果要给它一个形态的话,可以用[] 代表 w = tf.Variable(tf.zeros([3]), dtype=tf.float32) #由于x是一个三维张量,w也需要相应的是一个形态为[3] 的三维向量 # tf.zeros() 函数可以生成一个值全为0的向量,即tf.zeros([3])的返回值是 [0,0,0],这个向量将作为w的初始值 n = x * w # ”*”代表数学中矩阵的点乘 —— 两个形态相同的矩阵中 每个相同位置的数字相乘 # 点乘和矩阵点乘是一样的 y = tf.reduce_sum(n) # 把作为它参数的张量【以后可能是矩阵】中的所有维度的值相加求和 loss = tf.abs(y - yTrain) optimizer = tf.train.RMSPropOptimizer(0.001) train = optimizer.minimize(loss) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) result = sess.run([train, x, w, y, yTrain, loss], feed_dict={x: [90, 80, 70], yTrain: 85}) # 在喂数据的时候,直接喂一个 三维向量就可以了,修改输出结果数组 print(result) result = sess.run([train, x, w, y, yTrain, loss], feed_dict={x:[98, 95, 87], yTrain: 96}) print(result)
[None, array([90., 80., 70.], dtype=float32), array([0.00316052, 0.00316006, 0.00315938], dtype=float32), 0.0, array(85., dtype=float32), 85.0] [None, array([98., 95., 87.], dtype=float32), array([0.00554424, 0.00563004, 0.0056722 ], dtype=float32), 0.88480234, array(96., dtype=float32), 95.1152]
从输出信息中可以看到x 、w 确实被理解成为一个数组
循环5000次:
import tensorflow as tf x = tf.placeholder(shape=[3], dtype=tf.float32) yTrain = tf.placeholder(shape=[], dtype=tf.float32) w = tf.Variable(tf.zeros([3]), dtype=tf.float32) n = x * w y = tf.reduce_sum(n) loss = tf.abs(y - yTrain) optimizer = tf.train.RMSPropOptimizer(0.001) train = optimizer.minimize(loss) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) for i in range(5000): result = sess.run([train, x, w, y, yTrain, loss], feed_dict={x: [90, 80, 70], yTrain: 85}) print(result) result = sess.run([train, x, w, y, yTrain, loss], feed_dict={x:[98, 95, 87], yTrain: 96}) print(result)

可以看到误差已经缩小到很小的范围,三个权重分别接近 0.6 0.3 0.1
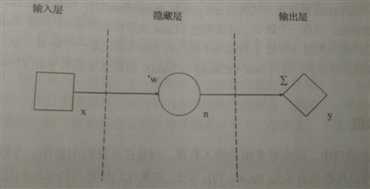
我们使用向量来组织输入数据后,只用一个神经元就解决了原来需要三个神经元的问题
对于一个普通数字,我们把它叫做“标量”,这个数字可以是整数或者浮点数(小数)
比如,之前的 yTrain 就是一个典型的标量,因为它代表的是总分数
但是 yTrain 在输出中显示是数组类型,而向量在计算机中 也是用数组类型表示的 ———— 解释:
x w 的表达形式类似 array([98.,95.,87.],dtype=float32)
yTrain 的表达形式类似 array(96.0,dtype=float32),虽然也是array,但是其中没有[] 包括的数组,只有一个数字。这说明,把 yTrain 标记为 array 只是 TensorFlow 的理解方式问题,其实质还是标量
向量在计算机中 是用 一个数组来表示的,例如一个学生的分数 [90,80,70],那么两个学生的分数如何表示? —— > 矩阵

该 2X3 矩阵 第一行即第一位学生的成绩,第二行 即第二位学生的成绩
# 计算机中不直接支持矩阵这种数据类型,但是可以用“二维数组”满足这种表达要求
x = [[90,80,70],[98,95,87]]
或者这么写
x1 = [90,80,70] x2 = [98,95,87] x = [x1,x2]


比如:
[[[90,80,70],[98,97,95]],[[70,75,78],[60,65,68]]]
这个三维数组可以用来表达两个班级的学生的总成绩,第一个维度包含了两个班级,第二个维度是两个学生,第三个维度中包含 3 科成绩【3个数字】
张量 主要是用来存放节点的输出数据的,其中存放的数据可以是一个标量【一个数】,也可以是一个向量【一组数】,还可以是一个矩阵【二维数组】,甚至用多维数组来表达的数据
TensorFlow 中 用 形态 shape 来表达在张量中存储的数据的形式
形态本身也是用一个类似一维数组的表达形式来表示的

如果张量存储的是上方的二维数组,可以说他的形态是 [2,3] ———— 可以看出,形态本身也是一个一维数组,2 3 分别表示这个矩阵两个维度(行和列)上的项数 —— (2,3) 也可以用来表示该形态
[90,80,70]
形态是 [3] —— 只有1个维度,维度中项数是3,就是说有3个数字
对于一个标量,也就是一个数字 ———— [] 或 () 来表示形态
[[[90,80,70],[98,97,95]],[[70,75,78],[60,65,68]]]
形态是 ———— [2,2,3]
在TensorFlow 中,张量的形态可以用一个数组来表示,这个数组中 有几个数字,就说这个张量是几“价”的张量 ———— 标量 0价 向量 1价 二维数组 2价 三维数组 3价
TensorFlow 会在程序执行时,根据输入的数据自动确定张量的形态。。。举例:
import tensorflow as tf x = tf.placeholder(dtype=tf.float32) xShape = tf.shape(x) sess = tf.Session() result = sess.run(xShape, feed_dict={x: 8}) print(result) result = sess.run(xShape, feed_dict={x: [1, 2, 3]}) print(result) result = sess.run(xShape, feed_dict={x: [[1, 2, 3], [3, 6, 9]]}) print(result)
[] [3] [2 3]
在这段代码中,我们定义了一个占位符变量 x,但没有指定它的形态
为了查看x 的实际形态,定义了一个变量 xShape ,通过传入参数 tf.shape(x) 即可得到 x 的形态
直接运行会话,三次给x 输入不同形态的数据 ———— 标量(一个数字) 、向量(一维数组)、二维数组 —— 程序的输入也符合预想
严格规范输入数据,可以定义张量时 指定形态:
import tensorflow as tf x = tf.placeholder(shape=[2, 3], dtype=tf.float32) xShape = tf.shape(x) sess = tf.Session() result = sess.run(xShape, feed_dict={x: [[1, 2, 3], [2, 4, 6]]}) print(result) #给张量“喂”不符合形态的数字会报错 result = sess.run(xShape, feed_dict={x: [1, 2, 3]}) print(result)

总结:各种形态在TensorFlow中的表达:
#标量
x1 = tf.placeholder(shape=[], dtype=tf.float32) x2 = tf.placeholder(shape=(), dtype=tf.float32)
#向量 x3 = tf.placeholder(shape=[3], dtype=tf.float32) x4 = tf.placeholder(shape=(3), dtype=tf.float32) x5 = tf.placeholder(shape=3, dtype=tf.float32) x6 = tf.placeholder(shape=(3, ), dtype=tf.float32)
#二维数组(二阶张量) x7 = tf.placeholder(shape=(2, 3), dtype=tf.float32) x8 = tf.placeholder(shape=[2, 3], dtype=tf.float32) sess = tf.Session() result = sess.run(tf.shape(x1), feed_dict={x1: 8}) print(result) result = sess.run(tf.shape(x2), feed_dict={x2: 8}) print(result) result = sess.run(tf.shape(x3), feed_dict={x3: [1, 2, 3]}) print(result) result = sess.run(tf.shape(x4), feed_dict={x4: [1, 2, 3]}) print(result) result = sess.run(tf.shape(x5), feed_dict={x5: [1, 2, 3]}) print(result) result = sess.run(tf.shape(x6), feed_dict={x6: [1, 2, 3]}) print(result) result = sess.run(tf.shape(x7), feed_dict={x7: [[1, 2, 3], [2, 4, 6]]}) print(result) result = sess.run(tf.shape(x8), feed_dict={x8: [[1, 2, 3], [2, 4, 6]]}) print(result)
[] [] [3] [3] [3] [3] [2 3] [2 3]
介绍一个 常用的规范化可变参数的小技巧
之前的三好学生问题: 总分 = x1 * w1 + x2 * w2 + x3 * w3 —— 其中权重之和 w1+w2+w3 = 1
或者用一个3维变量 w表示这些权重,那么对三维变量w求和应该 = 1,把这个规则应用程序中,可以大幅度减少 优化器调整可变参数的工作量
import tensorflow as tf x = tf.placeholder(shape=[3], dtype=tf.float32) yTrain = tf.placeholder(shape=[], dtype=tf.float32) w = tf.Variable(tf.zeros([3]), dtype=tf.float32) wn = tf.nn.softmax(w) n = x * wn y = tf.reduce_sum(n) loss = tf.abs(y - yTrain) optimizer = tf.train.RMSPropOptimizer(0.1) train = optimizer.minimize(loss) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) for i in range(2): result = sess.run([train, x, w, wn, y, yTrain, loss], feed_dict={x: [90, 80, 70], yTrain: 85}) print(result[3]) result = sess.run([train, x, w, wn, y, yTrain, loss], feed_dict={x:[98, 95, 87], yTrain: 96}) print(result[3])
[0.33333334 0.33333334 0.33333334] [0.413998 0.32727832 0.2587237 ] [0.44992 0.32819405 0.22188595] [0.5284719 0.2905868 0.18094125]
由以上输出的结果(即wn ,可以明显看到wn 的变化情况)
wn = tf.nn.softmax(w)
nn 是neural network的缩写,nn 是tensorFlow 的一个重要的子类(包)。soft 函数 可以把一个向量规范化后得到一个新的向量,这个新的向量中的所有暑之相加起来保证为1
soft 函数的这个特性经常被用来在神经网络中处理分类的问题,但在这里,暂时只让它满足让所有权重值相加和为1的需求。
wn 的各个值项相加总和为1,并且它的形态与w完全相同
也可以把 w1 w2 w3组成一个向量再输入: wn = tf.nn.softmax([w1,w2,w3])
经过 softmax 函数运算后,会发现达到相同误差率所需要的训练次数明显减少
本节和上一节研究的三好学生问题,是一个典型的线性问题。符合 y = w*x
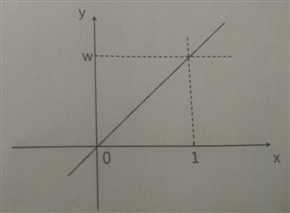
计算结果是一条直线的问题就叫做线性问题
其中 x y w可以是标量,向量,甚至矩阵数据
但是,现实问题不可能都是经过原点的线性问题,所有实际上使用 y = w * x + b 这样适应性更强的线性模型公式来处理问题
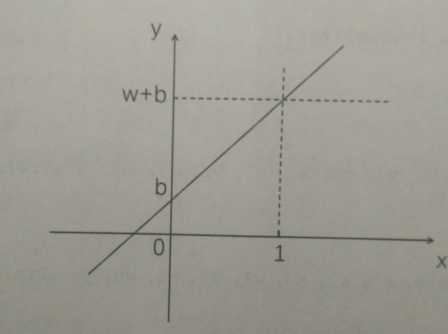
参数b ,称为 偏移量或偏置值。
线性模型虽然无法解决线性问题,但是在解决非线性问题时,我们通常仍然会 用线性模型作为神经元节点处理中的第一步,再做非线性化的处理。
标签:误差 工作 loss 小技巧 总结 优化 权重 特性 原因
原文地址:https://www.cnblogs.com/expedition/p/11515185.html