标签:就是 带来 定义 多个 完全 方向 主程 阶乘 inf
1:为什么要用函数
2:为什么要用函数重载
3:什么是值传递
4:什么是地址传递
5:递归函数
1:函数会让我们的主程序看起来更加的简便,更加的明了,让我们的程序结构更加简单。
2:函数可以反复被调用,当我们下次想在使用的时候,不用再去编写。
eg: 当我们计算a的n次方时
当我们不使用函数时,程序如下:
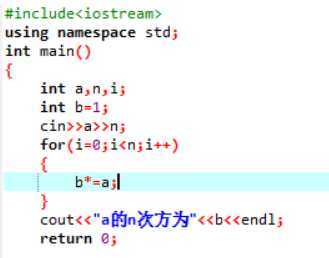
当我们使用函数时,程序如下:
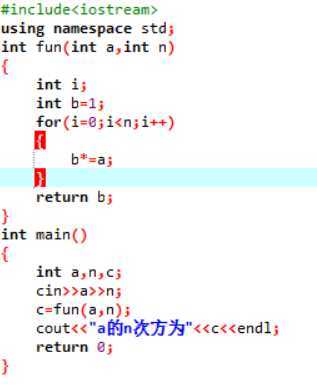
可知,当我们使用函数时代码会更加简单明了,且当我们下次想计算另外的次方运算时会更加简便,可以直接调用函数。
若没有函数重载机制,那么对不同类型的数据进行相同的操作时也需要定义名称完全不同的函数。这样在调用的时候会给我们带来极大的不便,而用函数重载会帮助我们解决这类问题
eg:
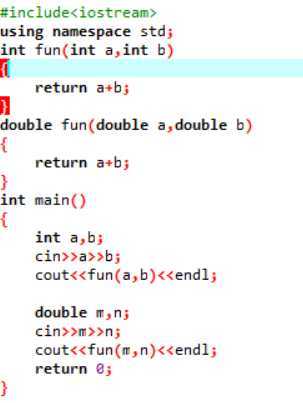
当我们采取函数重载的时候,我们可以根据参数表,即参数的个数或数据类型可以不同,自动调用对应的函数。 这样就不需要我们写多个程序来采取运算。
在这种情况下传给形参的是变量的值,传递方向是单向的。即如果在执行函数期间形参的值发生变化,并不传回给实参,这就是值传递。(因为在函数调用期间,形参和实参不是同一个存储单元)
eg:
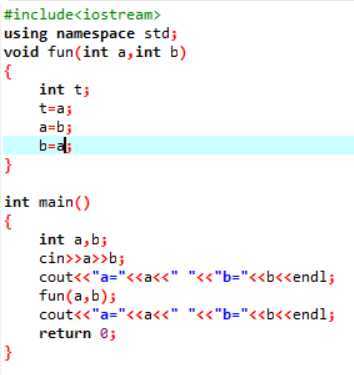
可以看出,函数在进行值传递的时候无论形参的值怎样发生改变,都不会影响到实参的结果
地址传递是一种将参数地址传递的方式,这样就可以使过程访问到实际的变量。结果就是过程中可以改变变量的真正值,但是其本质上也是值传递。比方说,有两个箱子AB,但是箱子在我这里,A和B中都有你想要的东西,我把A里面的东西直接给你就是值传递,我把B箱子的钥匙给你就是地址传递。
eg:
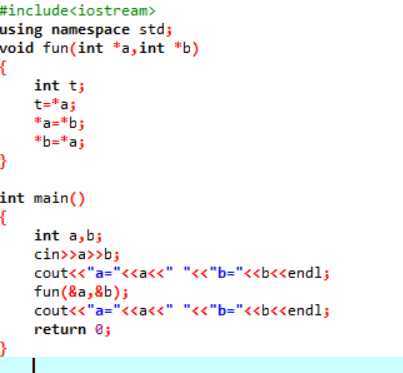
由上面程序可以看出,这种地址传递在函数中改变的不是实参的值,而是实参地址所指向的变量的值,在这种方式中实参的值是变量的地址。
一个函数在他的函数内调用自身被叫做递归调用,而这个函数被称为递归函数。他反复调用自身,每调用一层就进入新的一层。递归函数在一定程度上可以剪短我们的代码长度。
注意:
我们在运用递归函数的时候首先我们要知道“出口”在哪,知道这个初始值,并且找到对应的递归关系,才能很好的书写并调用递归函数。
eg:
我们通过一个求阶乘的例子来看递归函数的调用:
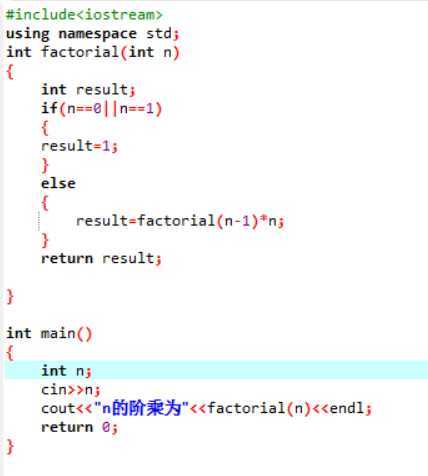
注意:为了防止递归函数为终止的进行,必须在函数内加有终止递归调用的手段。常用的办法是加条件判断。虽然递归函数极大节省了代码长度,但是递归调用不仅难于理解,而且开销也较大,效率并不高需要一层一层推进。
标签:就是 带来 定义 多个 完全 方向 主程 阶乘 inf
原文地址:https://www.cnblogs.com/byp-520/p/11520772.html