标签:ret update btn cout 时间 代码 flow 输入格式 技术
如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含四个正整数ui、vi、wi、fi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi),单位流量的费用为fi。
一行,包含两个整数,依次为最大流量和在最大流量情况下的最小费用。
4 5 4 3 4 2 30 2 4 3 20 3 2 3 20 1 2 1 30 9 1 3 40 5
50 280
时空限制:1000ms,128M
(BYX:最后两个点改成了1200ms)
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=5000,M<=50000
样例说明:
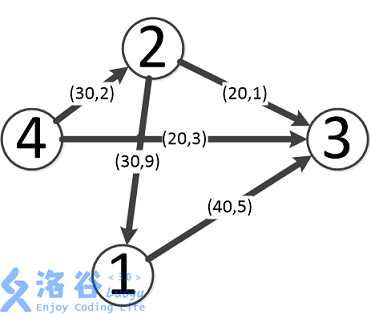
如图,最优方案如下:
第一条流为4-->3,流量为20,费用为3*20=60。
第二条流为4-->2-->3,流量为20,费用为(2+1)*20=60。
第三条流为4-->2-->1-->3,流量为10,费用为(2+9+5)*10=160。
故最大流量为50,在此状况下最小费用为60+60+160=280。
故输出50 280。
在最大流的E-K求法中,我们遍历全图,找到一条可增广的路径。那么在最大流不变时,每段费用越少越优,所以我们可以使用SPFA来代替DFS,此外因为有负值的存在,使用dij会比较麻烦,因而选择SPFA。时间复杂度上线为O(nm^2)。
#include<bits/stdc++.h> #define N 10700 #define M 107000 #define inf 1<<29 using namespace std; struct node{ int y,z,p,next; }e[M*2]; int tot=1,head[N],maxflow=0,ans=0; int n,m,s,t; void add(int x,int y,int z,int p){ e[++tot].y=y;e[tot].z=z;e[tot].p=p;e[tot].next=head[x];head[x]=tot; e[++tot].y=x;e[tot].z=0;e[tot].p=-p;e[tot].next=head[y];head[y]=tot; } int incf[N],v[N],pre[N],d[N]; bool spfa(){ queue<int> q; memset(d,0x3f,sizeof(d)); memset(v,0,sizeof(v)); q.push(s);d[s]=0;v[s]=1; incf[s]=inf; while(q.size()){ int x=q.front();v[x]=0;q.pop(); for(int i=head[x];i;i=e[i].next){ int y=e[i].y,z=e[i].z; if(!z) continue; if(d[y]>d[x]+e[i].p){ d[y]=d[x]+e[i].p; incf[y]=min(incf[x],z); pre[y]=i; if(!v[y]) v[y]=1,q.push(y); } } } if(d[t]==0x3f3f3f3f) return false; return true; } void update(){ int x=t; while(x!=s){ int i=pre[x]; e[i].z-=incf[t]; e[i^1].z+=incf[t]; x=e[i^1].y; } maxflow+=incf[t]; ans+=d[t]*incf[t]; } int main() { int x,y,z,p; cin>>n>>m>>s>>t; for(int i=1;i<=m;i++){ scanf("%d%d%d%d",&x,&y,&z,&p); add(x,y,z,p); } while(spfa()) update(); cout<<maxflow<<" "<<ans<<endl; return 0; }
标签:ret update btn cout 时间 代码 flow 输入格式 技术
原文地址:https://www.cnblogs.com/wangyiding2003/p/11524206.html