标签:关系 二维 最优 防御 进入 维数 最大流 dna 肩膀
克雷数学研究所(Clay Mathematics Institute,CMI)是在1998年由商人兰顿·克雷(Landon T. Clay)和哈佛大学数学家亚瑟·杰夫(Arthur Jaffe)创立,兰顿·克雷资助的一家非牟利私营机构,总部在麻萨诸塞州剑桥市,机构的目的在于促进和传播数学知识。克雷数学研究所给予有潜质的数学家各种奖项和资助,该研究所在2000年5月24日公布的七个千禧年难题,它们是:
(1)霍奇猜想
(2)庞加莱猜想
(3)黎曼假设
(4)杨-米尔斯规范场存在性和质量间隔假设
(5)NS方程解的存在性与光滑性
(6)贝赫和斯维讷通-戴尔猜想
(7)P=NP?
这七个问题被研究所认为是“重要的经典问题,经许多年仍未解决”。解答任何一题的第一个人将获颁予一百万美元奖金,所以这七个问题共值七百万美元。
近20年过去了,在这7个问题中,只有庞加莱猜想得到了解决。对于普通的程序员来说,前6个难题或许过于遥远,但是你一定听说过NP问题的大名。
在我读高中的时候,小浣熊干脆面中的水浒英雄卡曾经风靡一时。当时1998年央视版的《水浒传》刚开播不久,再加上课本上《鲁提辖拳打镇关西》和《林教头风雪山神庙》的助攻,同学们收集英雄卡的热情空前高涨。
卡片虽然精美,但是每袋干脆面只有一张英雄卡,想要收集齐全颇为不易。一个快速收集的办法就是多买干脆面。当时的高中生并没有多少零花钱,最富裕的同学也不过每天买两袋。在收集时也发现了另一个问题,如果在同一家店买,那么得到重复英雄卡的几率会大大增加,有个运气极差的同学连吃了两星期干脆面,居然得到了十几张豹子头林冲。
住校的同学纷纷求助于我这种走读生,于是我每天多了一个任务,在上学路上的每一所食杂店购买小浣熊干脆面。
英雄卡的人物渐渐丰富起来,大家还互相交换,只是到了毕业,仍然没有人把全套英雄卡收集齐全。
回顾水浒英雄卡的故事,无论是加大购买量还是扩大购买范围,都很难达成“收集全套卡片”的最终目标,整个过程费时费力又费钱,还需要很大的运气成分。如果没有网购平台,我甚至都不知道是否真有人能够集全。
水浒英雄卡的故事就是一个P/NP问题,它的焦点在于,集全英雄卡的过程是否能够变得轻而易举?
计算机可以帮助我们解决很多问题,但是仍有一部分问题可能永远无法通过简单的计算得到答案,试着解答它们是计算机科学家和数学们的重要挑战。人们给这类问题了一个奇怪的名字——P/NP问题。
我们讨论的“有效”算法几乎都是多项式时间算法,P/NP中的P就是指多项式时间(Polynomial)。一个复杂问题如果能在多项式时间内解决,它就被称为P问题,这意味着计算机很容易求解。
NP问题就是除了P问题之外的问题吗?如果是就好了。世界总是很复杂,有时候我们并不用能证明一个问题能在多项式时间内解决,同时也没法证明它不能在多项式时间内解决,也就是说这个问题是悬案,在当下看起来没法有效解决,但是谁也说不准在未来是否能很容易解决。对于这类问题,简单地归为非P类问题就不和合适了,就像我们无法把建立月球基地和建立银河星系联盟归为非P类问题。
NP问题不是非P类问题,NP不是“Not P”的意思,NP指非确定性多项式时间(nondeterministic polynomial)。NP问题强调的不是“是否能在多项式时间内找到解”,而是“是否能够在多项式时间内验证解”,如果一个问题的解可以在多项式的时间内被验证,那么这个问题就是NP问题。
我们在 密码疑云 (3)——详解RSA的加密与解密 中曾提到了RSA加密机制的原理:“将两个大素数相乘很容易,但是想要对它们的乘积进行素因子分解却极其困难”。假如有人告诉你3999991可以分解成两个素数的乘积,也许你不知道可以分解成哪两个素数,但是如果告诉你这两个素数是1997和2003,那么你很容易计算出1997×2003=3999991。
大整数的素因子分解就是典型的NP问题,有没有多项时间的分解算法并不重要,重要的是如果有人给了你两个素数,你很容易验证这两个素数的乘积是否是那个大整数。这符合一般的认知:在大多数时候,验证一个解比得到一个解更容易。
既然能在多项式时间内解决一个问题,必然也能在多项式时间内验证这个问题的解,这意味着所有的P问题都是NP问题,P∈NP。
大约在公元前4200年,古代埃及人按尼罗河水的涨落和农作物生长的规律,把一年分为泛滥季、耕种季、收获季3个季节,每季分为4个月,每月30天,岁末增加5天节日,共计365天。
5000多年前,中国就有《阴阳历》,每年366天。魏晋南北朝(公元220年~公元518年)时期,祖冲之制定《大明历》,首次将岁差计算入内,每年365.2428天,与现在的精确测量值仅相差52秒。
古代玛雅人已经知道了一些天体的精确运行周期,他们测得太阳年的长度是365.2420天,比现代的测量值365.2422只至少了0.0002天,相当于17.28秒。
经过漫长的岁月,不同的文明在不同的时期分别独立发现了地球公转的规律,从而制定了历法,这至少从哲学上证明“历法”这一概念是真实存在的。类似地,在不同时期的人们对很多不同领域问题的研究中,也都不约而同地提出了相同的问题——是否所有的NP问题都是P问题?也就是说,是否所有能够在多项式时间内验证的问题都可以在多项式时间内解决?这个问题被简称为“P=NP?”
所谓的“P/NP问题”,其实就一句话:证明或推翻P=NP。只要证明一个任意规模下的NP问题都可以在多项式时间内求解,就可以说对于该问题P=NP,即该问题是一个P问题。
我经常听到程序员们在讨论问题时说:“××是NP问题,只能用蛮力法。” 程序员们的说法并不完全准确,NP问题可没有强调非得用蛮力法,只强调了在有解的情况下可以轻松地验证解,他们真正指的应该是NPC问题。
NPC问题也称NP完全问题,是NP-Complete的缩写。NPC问题满足两点,首先,NPC问题肯定也是NP问题;其次,所有NP问题都能够在多项式时间内规规约到NPC问题。为什么要将NP问题规约到NPC问题呢?这是因为人们发现某些NP问题的复杂性与整个类的复杂性相关联,如果这些问题中的任何一个存在多项式时间的算法,那么所有该类问题都是多项式时间可解的。这也符合常理,NPC问题是NP问题规约来的,所以NPC问题的难度一定大于NP问题,只要能在多项式时间内解决NPC问题,那么NP问题也能在多项式时间内解决,此时NP问题也就变成了P问题,P=NP。
在《西游记》的第二回中,孙悟空学成本领回到花果山后,得知很多猴子猴孙被混世魔王掳走,连水帘洞中的石盆、石碗也被抢了去。大怒的孙悟空在混世魔王的老巢将其“照顶门一下,砍为两段。领众杀进洞中,将那大小妖精,尽皆剿灭。”在解救了众猴后,对众道:
“汝等跟我回去。”众猴道:“大王,我们来时,只听得耳边风声,虚飘飘到于此地,更不识路径,今怎得回乡?”悟空道:“这是他弄的个术法儿,有何难也!我如今一窍通,百窍通,我也会弄。你们都合了眼,休怕!”
花果山的小猴们显然没法在多项式时间内“弄的个术法儿”,但是能很容易验证“弄的个术法儿”的结果,就是“只听得耳边风声,虚飘飘到于此地”,因此可以把混世魔王的法术看作NP问题。至于孙悟空,在学艺时从没把猴子或类似的动物摄到空中,只修习了筋斗云和七十二变,但由于七十二变是高端的NPC法术,因此“一窍通,百窍通”,不仅能顺利地把众猴带回花果山,还在后续的大闹天宫和西天取经路上施展过诸如三头六臂、身外身、隐身法、定身术、元神出窍、法天象地、担山赶月等其他NP法术。
NPC问题是在P问题与NP问题上的一个重大进展,问题是,想要在NPC问题上找到一个多项式时间内的算法出奇地困难,难倒人们甚至不相信存在这样的算法,就像孙悟空的“一窍通,百窍通”一样,反正我没见过谁能做到。
另一个具有代表性的NPC问题是销售员旅行问题(traveling salesman problem)。一个推销员要从北京出发,经过上海、南京、杭州、南昌、广州等n个城市,最后返回北京。每两个城市之间都有直达的飞机、高铁等交通工具。销售员的交通费用预算是Q,他在每个城市仅驻留一次,是否存在这样一个行程,销售员既能遍历所有城市,又能让总费用小于Q?
有人说这还不简单?从北向南走就好了。现实生活中也许我也会这么安排,但是加上预算费用后就不是那么回事了。虽然上海到南京很近,但也许正好有一趟上海到广州的特价航班,这时候又该怎么选择呢?如果用蛮力法遍历,3个城市间会产生2!种路线,10个城市会产生9!=362880种路线,20个城市会产生19!≈1.21×1017种路线,在这么多种路线中挑选,简直太可怕了。
销售员旅行问题可以规约为图论中一个著名的问题,已给一个n个点的完全图(图中每两个顶点之间都存在权值已知的边),求每个顶点正好遍历一次,且总权值小于某个值的封闭回路。这是一个NPC问题,迄今为止仍未一个找到一个能够应对大型问题的有效算法。正是由于NPC问题的存在,才使人们普遍相信P≠NP。
NP-hard问题也称NP难题,从名字就知道,它是NP家族中最难的。NPC问题属于NP-hard问题,所以NP-hard问题肯定没有能在多项式时间内找到解算法,至少目前没有。NP-hard问题之所以hard,是因为对于一些NP-hard问题来说,即使给出解,也难以在多项式时间内验证,所以NP-hard问题未必是NP问题。
“难以在多项式时间内找到解”容易理解,“即使给出解,也难以在多项式时间内验证”又是怎么回事呢?我们把销售员旅行的问题稍作修改,求使销售员能遍历所有城市,每个城市仅驻留一次,且总费用最小的行程。首先可以确定至少目前为止还不存在有效的算法,现在给了你一个解并告诉你这就是最终解,你如何确定它的正确性呢?办法大概还是遍历,把这个解与所有其它行程比对,从而确定它是否是最优的,验证解的复杂度仍然是n!。
NP、NPC、NP-hard的关系:
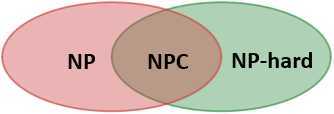
从广义来说,在承认P≠NP的前提下,NP问题也指难以在多项式时间内求解的问题(本章所指的NP问题都广义的NP问题)。在实际工作中,我们经常会遇到很难解决的问题,如果这些问题是NP问题,又该怎么办呢?
琪琳是“甜品之家”的程序员,她为公司编写了一个甜品创新的程序,这个程序能够微调各种配料,找到最具口感的甜品。公司使用这个程序开发了一系列爆款的产品,大赚了一笔。经理最近突发奇想,打算制作一款“风味独特”的小甜饼,这款小甜饼不仅能够满足所有人的味蕾,甚者能让一个独眼蛤蟆开心地笑起来。但是这次,被寄予厚望的程序失灵了,这可难坏了琪琳,连续加班一个月都没有丝毫进展。另一公室的刘闯得知了情况,拍拍琪琳的肩膀说:“这很明显是个NP问题,科学家都不相信有办法解决。别浪费脑细胞了,咱们一起去打乒乓球吧!” 琪琳恍然大悟,真的去打乒乓球了。没过多久,经理就以“工作不负责任”为由,扣掉了她的项目奖金。
对于NP完全问题,虽然我们确信无法找到一个快速的解决方案,但生活仍要继续,问题还是要解决,此时不妨试试下面的7个办法。
1. 缩小问题规模
NP完全问题之所以困难,最重要的原因之一就是搜索规模过于庞大,因此适当地缩小问题规模就成了需要首先思考的问题。
在构建机器学习模型时,经常面对过于复杂的数据特征,这就需要用到数据降维技术。 数据降维,是解决数据“维数灾难”的有效手段,即通过某种数学变换将原始高维属性空间转变为一个低维的“子空间”,从而极大地缩小的原始问题的规模。
实际上“降维”并不仅仅存在于机器学习和科幻小说中,它就在我们身边。《三国演义》为我们铺开了近100年的历史画卷,这里既有军阀割据的混战,又有政治和军事的争斗,更有叱诧风云的英雄人物。神奇的是,这些多维度的故事通过“文字”这一工具实现了有效的降维,从而有效缩小了问题的规模,最终呈现在平面媒体上。
除了降维外,设置约束条件也是缩小问题规模的有效手段。
在《三体2·黑暗森林》中,作为“面壁者”逻辑向大史提出了一个NP问题——找一个二十岁左右的梦中女孩儿:
罗辑啜了一口酒,坐到史强身边:“大史啊,我求你帮个忙。在你以前的工作中,是不是常常在全国甚至全世界范围找某个人?”“是。我对此很在行,找人吗?”“当然。那好,帮我找一个人,一个二十岁左右的女孩儿,这是计划的一部分。国籍、姓名、住址?都没有,她甚至连在这个世界上存在的可能性都很小。”大史看着罗辑,停了几秒钟说:“梦见的?”罗辑点点头:“包括白日梦。”
这个“二十岁左右的女孩儿”是逻辑梦中的完美女友,人海茫茫,能否找到只能看缘分,甚至是否存在都说不准,估计绝大多数人都会拒绝或敷衍这个找人的请求。但是阅人无数的大史警官并没有回绝,而是尝试让客户捋清需求,问清这个女孩的具体长相、爱好和其他属性:
“她是一个,嗯,东方女孩,就设定为中国人吧。”罗辑说着,拿出纸和笔画了起来,“她的脸型,是这个样子;鼻子,这样儿,嘴,这样儿,唉,我不会画,眼睛……见鬼,我怎么可能画出她的眼睛?你们是不是有那种东西,一种软件吧,可以调出一张面孔来,按照目击者描述调整眼睛鼻子什么的,最后精确画出目击者见过的那人?”
“有啊,我带的笔记本里就有。”
“那你去拿来,我们现在就画!”
大史在沙发上舒展一下身体,让自己坐得舒服些,“没必要,你也不用画了,继续说吧,长相放一边,先说她是个什么样的人。”
罗辑体内的什么东西好像被点燃了,他站起来,在壁炉前躁动不安地来回走着,“她……怎么说呢?她来到这个世界上,就像垃圾堆里长出了一朵百合花,那么……那么的纯洁娇嫩,周围的一切都不可能污染她,但都是对她的伤害,是的,周围的一切都能伤害到她!你见到她的第一反应就是去保护她……啊不,呵护她,让她免受这粗陋野蛮的现实的伤害,你愿意为此付出一切代价!她……她是那么……唉,你看我怎么笨嘴笨舌的,什么都没说清。”
“都这样。”大史笑着点点头,他那初看有些粗傻的笑现在在罗辑的眼中充满智慧,也让他感到很舒服,“不过你说得够清楚了。”
“好吧,那我接着说,她……可,可我怎么说呢?怎样描述都说不出我心中的那个她。”罗辑显得急躁起来,仿佛要把自己的心撕开让大史看似的。
逻辑提供了一大堆无助解决问题的信息,仅仅是在需求外围打转,这种场景是否似曾相识?于是大史开始引导逻辑:
大史挥挥手让罗辑平静下来,“算了,就说你和她在一起的事儿吧,越详细越好。”
罗辑吃惊地瞪大了双眼,“和她……在一起?你怎么知道?”
大史又呵呵地笑了起来,同时四下看了看,“这种地方,不会没有好些的雪茄吧?”
“有有!”罗辑赶忙从壁炉上方拿下一个精致的木盒,从中取出一根粗大的“大卫杜夫”,用一个更精致的断头台外形的雪茄剪切开头部,递给大史,然后用点雪茄专用的松木条给他点着。
大史抽了一口,惬意地点点头,“说吧。”
罗辑一反刚才的语言障碍,滔滔不绝起来。他讲述了她在图书馆中的第一次活现,讲述他与她在宿舍里那想象中的壁炉前的相逢,讲她在他课堂上的现身,描述那天晚上壁炉的火光透过那瓶像晚霞的眼睛的葡萄酒在她脸庞上映出的美丽。他幸福地回忆他们的那次旅行,详细地描述每一个最微小的细节:那雪后的田野、蓝天下的小镇和村庄、像晒太阳的老人的山,还有山上的黄昏和篝火……
在收集到一些信息后,大史开始缩小问题规模,将复杂的描述拆解成一个个定类属性:
大史听完,捻灭了烟头说:“嗯,基本上够了。关于这个女孩儿,我提一些推测,你看对不对。”
“好的好的!”
“她的文化程度,应该是大学以上博士以下。”
罗辑点头,“是的是的,她有知识,但那些知识还没有达到学问的程度去僵化她,只是令她对世界和生活更敏感。”
“她应该出生在一个高级知识分子家庭,过的不是富豪的生活,但比一般人家要富裕得多,她从小到大享受着充分的父爱母爱,但与社会,特别是基层社会接触很少。”
“对对,极对!她从没对我说过家里的情况,事实上从未说过任何关于她自己的情况,但我想应该是那样的!”
“下面的推测就是猜测了,错了你告诉我――她喜欢穿那种,怎么说呢,素雅的衣服,在她这种年龄的女孩子来说,显得稍微素了些。”罗辑呆呆地连连点头,“但总有很洁白的部分,比如衬衣呀领子呀什么的,与其余深色的部分形成挺鲜明的对比。”
“大史啊,你……”罗辑用近乎崇敬的目光看着大史说。
史强挥手制止他说下去,“最后一点:她个子不高,一米六左右吧,身材很……怎么形容来着,纤细,一阵风就能刮跑的那种,所以这个儿也不显得低……当然还能想出很多,应该都差不离吧。”
罗辑像要给史强跪下似的,“大史,我五体投地!你,福尔摩斯再世啊!”
大史站起来,“那我去电脑上画了。”
大史成功地将一个NP问题加上了若干约束条件,最后找到了这个女孩儿,名字叫庄颜,只是比幻想中的“她”多了淡淡的忧伤。
2. 绕过问题
在碰到难题时,除了积极面对外,我们也应当思考一下,问题是否真的有解决的必要?是否可以绕过问题直指目标?
在第一次世界大战后,法国为了防止德军入侵而在其东北边境地区构筑起了一道有钢筋混凝土建造而成的防线,防线内部拥有各式大炮、壕沟、堡垒、厨房、发电站、医院、工厂等,通道四通八达,较大的工事中还有有轨电车通道,这就是著名的马其诺防线。马其诺防线从1928年起开始建造,1940年才基本建成,造价50亿法郎。这道“完全防御”军事思想的防线被誉为“不可攻破的防线”。结果大家都知道了,德国人没有对着马其诺防线死磕,而是绕过防线,率领28个师穿入阿登山区进攻比利时、荷兰和卢森堡,还没等法国人来得及反应,德国军队就兵临巴黎城下,法国投降。
德国人的目标是占领法国,马奇诺防线是达到目标途中的一个难题,这个难题被轻易地绕开了。很多时候,“搬家”或许比“移山”更有效。
3. 转换问题
另一种值得一试的办法是把待解决的难题转换成另一个能够解决的问题。
密码疑云 (3)——详解RSA的加密与解密 中,Mallory并没有尝试破解“芒砀山系统”,而是通过一系列社会工程学的知识骗取了密码,从而轻易进入“号称能够安全运行100年”的系统。
最小二乘法(2)——多项式函数能够拟合非线性问题原理 中,我们介绍了泰勒展开,它将一个难以处理的积分转换成了无数个易于处理的简单积分,使用极限的思想求解,达到化质为量的目的。
网络流(3)——找到最小st-剪切 中,我们将多源点的押粮问题转换成了标准的最大流问题,用已掌握的知识求解。
4. 退而求其次
如果在通向目标的途中一定要解决某个NP困难问题,那么 搜索的策略(2)——贪心策略、A*搜索详解(1)——通往基地的最短路线 介绍的一些有启发性质的算法或许会提供一些参考;退而求其次(2)——遗传算法 的遗传算法还告诉我们,在必要的时候应当放弃寻找最优解,转而寻找可以接受的较好解。如果考不上清华、北大,其他“985”也不是不可接受。
5. 依赖计算机的高速运算
对于八皇后问题,1854年在柏林的象棋杂志上不同的作者发表了40种不同的解。今天,我们可以通过近乎蛮力的搜索找到全部的92种解。
1946年诞生的ENIAC,每秒只能进行300次各种运算或5000次加法。
2019年,美国的“顶点”,取代“神威太湖之光” 成为“世界第一计算机”,其预算速度为20亿亿次/每秒。
75年间,计算机的速度已经得到了极大的提升,虽然NP问题仍然是NP问题,但是技术的进步给了我们一战的勇气,让我们可以使用蛮力法处理一些中等规模的问题。
处理器运算速度的提升带给了我们更多的可能性。Square公司于1997年在PS上发行的角色扮演类游戏《最终幻想7》,尽管剧情优秀,但画质着实“感人”,但是在当年,那种充满方块感的画面仍然是PS平台上不可逾越的经典。2019年6月10日,Square Enix公司在美国洛杉矶举办了《最终幻想7》音乐会,宣布游戏《最终幻想7:重制版》将于2020年3月3日登陆PS4平台,并公布了游戏的宣传片。在宣传片中,游戏画面十分华丽,人物几可乱真。
计算机性能的提升可以帮我们解决相当一部分问题,这样看来,蛮力法也不是那么一无是处。
6. 尝试NC搜索
随着多核技术和分布式计算的发展,我们似乎更有勇气碰触一些过去的禁地。我们把那些能够通过并行计算快速找到答案的搜索称为NC搜索。然而遗憾的是,NP问题的规模也在扩大,我们今天面对的问题也比过去复杂得多,因此NC也不是万能药。
尽管在未来,NP是否能用NC仍然不得而知,但是NC搜索可以帮我们快速解决一些小规模的NP问题,或者在可接受的时间解决一些中等规模的NP问题。
7. 打乒乓球去吧
当上述方案都无效时,大概可以打乒乓球去了。
其实P/NP问题并不仅仅是一道数学难题,它更像是一种指导思想,一种根据问题的困难程度将问题分类的工具。当面对一个NP完全问题时,我们知道没有一个能够在所有情况下都解决该问题的算法,我们要做的并不死磕硬打,而是找到某些替代方法,做出某些“退而求其次”或“不得已而为之”的选择。
美国科幻作家艾萨克·阿西莫夫的小说《永恒的终结》讲诉了一个关于时空的神奇故事:27世纪,人类在掌握时间旅行技术后,创造了“时空壶”,并成立了一个叫做“永恒时空”的组织,在每个时代的背后,默默地守护着人类社会的发展。这一系列功劳都归功于24世纪的一个名叫马兰松的伟大科学家,正是他发明了时间力场,从而创造了“时空壶”。尽管马兰松的后人们一直在使用“时空壶”,但并不明白它的运作原理,因为作为“时间力场”理论基础的“列斐伏尔方程”在24世纪还没有出现!随着剧情的推进,最终揭示了完整的“因果链”——来自27世纪的库珀为24世纪带去了“列斐伏尔方程”,并从此留在24世纪,最终改名为马兰松。
欧几里得在著作《几何原本》时不曾想到会有内角和不等于180°的三角形。1830年前后,俄国数学家罗巴切夫斯基发表了关于非欧几何的理论,即后来的罗氏几何。在这种几何里,罗巴切夫斯基平行公理替代了欧几里得平行公理,即存在直线a及不在a上的一点A,过A点至少有两条直线与a共面且不相交。由此可演绎出一系列全无矛盾的结论,并且可以得出三角形的内角和小于180°。正是罗氏几何启发了爱因斯坦,成为发现广义相对论的基础。
对于NP问题来说,强调的是“不确定”是否在能做多项式时间内解决。随着科技的发展,过去“不确定”的问题在未来未必不可触及。既然P/NP问题的解决可能有赖于大幅度提升的理论和技术,那么我们不妨把希望寄托于未来,畅想一下P=NP的世界。
如果P=NP,基于NP完全问题的密码大厦将会瞬间倾塌,安全体系将会被重构;如果P=NP,电子游戏将不再局限于策划师设计好的剧本,而是像《安德的游戏》中的心理测试游戏一样,根据安德的选择做出自行演化;如果P=NP,DNA密码将被破解,生命之谜将被解开,人类将得到新一轮的进化;如果P=NP,机器人将被赋予更高级的智能,《银河帝国》将不再是幻想……到了那时,人类文明应当通向何方呢?
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公作者众号“我是8位的”

标签:关系 二维 最优 防御 进入 维数 最大流 dna 肩膀
原文地址:https://www.cnblogs.com/bigmonkey/p/11544242.html