标签:思想 下标 知识 bin 出现 异或 一起 不能 png
算法每日精进,offer!offer!offer!
给定一个包含,0,1,2,......,n 中 n 个数的序列,找出 0 - n中未出现的序列中的那个数。
如:
输入:[3, 0, 1]
输出:2
输入:[8, 5, 4, 6, 7, 1, 0, 2]
输出:3
方法一:对该序列排序,并遍历数组,下标与值不对应的那个下标就是缺失元素,时间复杂度,快排O(nlogn)
方法二:位运算
我们知道异或运算 , x ^ x = 0 , x ^ 0 = x
而且异或运算满足交换律和结合律,即 x ^ y ^ x = y ^ (x ^ x ) = y ^ 0 = y 如: 2 ^ 3 ^ 2 = 3 ^ (2 ^ 2) = 3 ^ 0 = 3
利用这两条特性,就可以在O(n)时间复杂度下解决该问题。
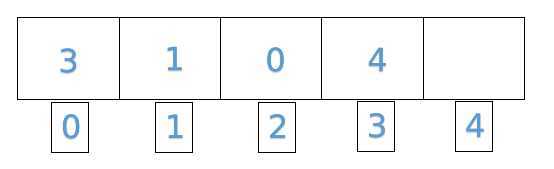
给出 0 - 4的一组序列,上述图例中很明显缺失了元素2,如果我们在遍历数组时将每个元素和其下标一起异或会是什么样的结果呢:
0 ^ 3 ^ 1 ^ 1 ^ 2 ^ 0 ^ 3 ^ 4^ 4 ^ 0 = (0 ^ 0) ^ (1 ^ 1) ^ (2 ^ 0) ^ (3 ^ 3) ^ (4 ^ 4) = 2
没想到这样一异或居然得到了缺失元素 2 。这样做的原理类似于消消乐,既然给出 0 - n的一个缺失某个元素的序列,那这个序列对应的下标值则是 0 - n(我们将最后一个下标为n的元素看做缺失元素,其值赋0( x ^ 0 = x,不影响计算结果)),
那么如此一来,序列中每个元素都一定有一个与其值相等的下标,而且最终有一个下标 找不到与它值相等的序列元素,这个下标就是我们所求的缺失元素。
而异或运算又满足交换律和结合律,这样两两一消,最终剩下的就是 为缺失元素占位的 0 与被没有被异或掉的那个下标值,再一异或得到的就是缺失元素。(如图例中的 2 ^ 0 )
时间复杂度:O(n)
方法三:数学公式
咳咳,这个题,换个没学过编程的人可能都可以在几分钟内给出答案,用一个数学公式就可以。
还记得等差数列求和公式吗?0 - n就是 一个公差为 1 的等差数列 ,根据公式我们可以得到 0-n所有元素求和的结果,再遍历含有缺失元素的序列累加求和,最终,两式相减自然得到的就是缺失元素
(初中生内心OS:菜鸡)
......
时间复杂度:O(n)
方法四:数学公式优化
菜鸡?nonono,等差数列求和公式要做乘法运算,如果只是简单的进行方法三,当n值很大的时候便会整型溢出!
出于细节,这是我们必须去考虑的一个问题。
这里给出优化,思想和方法二差不多,只不过这里不采用位运算,而是将下标与值相减,再将每次相减的结果相加,很显然加减法也可结合可交换,最终得到的结果就是缺失元素,而且也不会出现整型溢出问题。
Bingo !
还是方法二中给出的图,来试验一下:
(0-3) + (1-1) + (2-0) + (3-4) + (4-0) = (0-0) + (-3+3) + (1-1) + (2-0) + (-4+4) = 2
注意:这里无论采用下标减值还是值减下标都可以,但是这两种不能混用!
好了,今天说到这里,代码改天再补。
参考资料来自于:微信公众号 labuladong(非营销,贴出来是对知识和原创作者的尊重)
标签:思想 下标 知识 bin 出现 异或 一起 不能 png
原文地址:https://www.cnblogs.com/GuoYuying/p/11546244.html