有关多边形面积的总结

标签：向量   组成   cdn   strong   width   span   坐标   判断   矢量   

矢量矢量加减法：

设二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )。

则矢量加法定义为： P + Q = ( x1 + x2 , y1 + y2 )，同样的，矢量减法定义为： P - Q = ( x1 - x2 , y1 - y2 )。

矢量的点乘：

P=(x1, y1)，Q=(x2, y2)。则

向量的叉乘

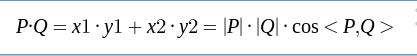
设矢量P = ( x1, y1 )，Q = ( x2, y2 )

则矢量叉积定义为由(0,0)、p1、p2和 p1+p2 所组成的平行四边形的带符号的面积。

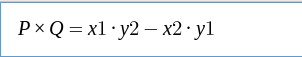
使用向量的叉乘可以判断向量的方向。

若 P × Q > 0 , 则P在Q的顺时针方向。

若 P × Q < 0 , 则P在Q的逆时针方向。

若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。

严格按照点的逆时针方向来算面积

这面积难道不重叠了吗？

注意，用叉乘算的三角形DEA + 三角形 DAB的值是负的， 而叉乘算的三角形 DBC的值是正的，等价于去掉了重叠部分。

 ans += (a[i] \* b[i + 1] - a[i + 1] \* b[i]);//a[]为x坐标，b[]为y坐标，模拟向量相乘

有关多边形面积的总结

标签：向量   组成   cdn   strong   width   span   坐标   判断   矢量   

原文地址：https://www.cnblogs.com/kamimxr/p/11559752.html