标签:pac class display 必须 高度 ace ice 有一个 计数器
有一排高楼,每一栋高楼有一个正整数高度,高度为 \(i\) 的概率为 \(2^{-i}\)。一栋楼的每层从下往上依次编号为 \(0,1,2,\cdots,i-1\)。
为了出题,大楼之间安装了溜索。在一栋楼的第 \(i\) 层和另一栋楼的第 \(i\) 层之间有一条溜索,当且仅当这两栋楼之间没有一栋大楼高度达到 \(i\) 层。
Alice 和 Bob 要数数有多少栋楼。
Alice 非常细心,她从最左侧的楼出发,计数器为 \(1\)。然后她向右移动,每经过一栋楼就将计数器 \(+1\)。
Bob 非常没耐心,他希望尽快数完。他从最左侧的楼出发,计数器为 \(1\)。他只使用溜索在大楼之间移动。Bob 会一直用最高的溜索向右移动,但由于恐高,他会忽略那些编号超过 \(h\) 的楼层。Bob 用溜索旅行跑得比香港记者还快,以至于他根本没法数清经过了多少栋楼,因此每经过一条溜索后只是将计数器 \(+2^i\),其中 \(i\) 是这条溜索所在楼层的编号。
举个例子。有 \(6\) 栋大楼,从左到右的高度分别是 \(1,4,3,4,1,2\),且 \(h=2\)。Alice 开始时计数器为 \(1\),并且将计数器加了五次 \(1\),得到的结果是 \(6\)。Bob 开始时计数器为 \(1\),然后他依次加上 \(1,4,4,2\),最终得到 \(12\)。注意,Bob 出于恐高忽略掉了最高的溜索。
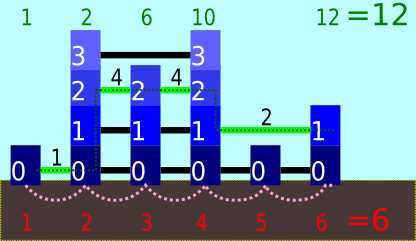
当 Alice 和 Bob 到达最右端的大楼时,他们将各自的计数器拿出来比较。给出 Alice 或者 Bob 的计数器的值,你需要计算出另外一个人的计数器的期望值。
\(2\le n\le 30000,\space 0\le h\le 30\)
二合一?
考虑一个子问题:\(Bob\) 每经过一条溜索,期望经过了多少栋楼。
设它的计数器累加了 \(2^h\),即溜索所在楼层的编号是 \(h\),高度是 \(h+1\)。那么中间那些楼的高度都必须 \(\le h\)。
设每一栋楼的高度\(\le h\) 的概率设为 \(p\),题目说了高度为 \(i\) 的概率是 \(2^{-i}\),则 \[p=\frac{1}{2}+\frac{1}{2^2}+\cdots+\frac{1}{2^n}=\frac{2^n-1}{2^n}=1-\frac{1}{2^i}\]
那么从一栋高度 \(\ge h\) 的楼的第 \(h\) 层出发走溜索,期望经过的高楼数就是 $$E=1\times p(中间没有小楼)\times p(最后一栋楼的高度
标签:pac class display 必须 高度 ace ice 有一个 计数器
原文地址:https://www.cnblogs.com/scx2015noip-as-php/p/cf335e.html