标签：target   端点   期望   部分   分类   ade   假设   htm   bsp   

期望得分：30+43+60

实际得分：0+43+60

rk13

A. 施工

看错题了，一是高度差的绝对值算了两遍，二是一次抬起一栋建筑。

正解：

• 手模发现5 1 2 5 的坑抬成 5 1 3 5是只会变差的，也就是对于一个凹下去的部分，答案取决于最深的位置。所以坑底一定是平的。
• 把坑抬到比两边高是不优的。显然

然后把式子拆开维护前缀和，最后算出对称轴判下合法性加点特判。

直接枚举决策点是O(n^2)的。

假设决策点是j，那么所有k的高度小于j+1~i-1，可以用一个单调递减的单调栈维护决策点。

详细见

B. 蔬菜

二维莫队可水，复杂度玄学。

正解四维偏序，平方转化点对。

C. 联盟

对于一条边，答案为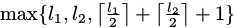即两棵树合并后的直径的端点，一定是四个端点中的两个。

如果我们预处理得到所有我们想要的子树中的最长链，那么我们就解决了

从原树的两个端点进行dp，这样我们得不到的子树中一定包含原树的直径。即使有多个直径亦是如此。

对于所有边按是否是直径上的边分类讨论。

最后断开任意一条答案边，再分别求下直径，输出直径中点（所有直径一定交于该点）

复杂度线性

主要考察树的直径性质和求法

csp-s模拟测试50

标签：target   端点   期望   部分   分类   ade   假设   htm   bsp   

原文地址：https://www.cnblogs.com/hzoi-yzh/p/11576175.html