标签：重要   完全   img   权重   随机   函数   泊松分布   正是   数字   

概念和性质

定义

期望是概率论中一个非常重要的概念。若 X 是一个离散型的随机变量，其分布列为 p(x)，那么 X 的期望记作 E[X]，定义为：

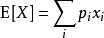
若 X 是一个连续型随机变量，其概率密度函数为 f(x)，则 X 的期望 E[X] 定义为：

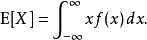
用语言表达，X 的期望就是 X 所有可能取值的一个加权平均，每个值的权重就是 X 取该值的概率。举个栗子：

若 X 的分布列为

　　　　　　　　　　　　　　　　　　　　　　p(0) = 1/2 = p(1)

那么

　　　　　　　　　　　　　　　　　　　　　　E[X] = 0 * 1/2 + 1 * 1/2 = 1/2

这正是 X 的两个可能取值 0 和 1 在通常意义下的平均值。另一方面，若

　　　　　　　　　　　　　　　　　　　　　　p(0) = 1/3, p(1) = 2/3,

那么

　　　　　　　　　　　　　　　　　　　　　　E[X] = 0 * 1/3 + 1 * 2/3 = 2/3

这是两个可能取值 0 和 1 的加权平均， 因为 p(1) = 2p(0)，此时 1 的权重是 0 的权重的 2 倍。

常见分布的期望

数学期望 E[X] 完全由随机变量 X 的概率分布所确定，若 X 服从某一分布，也称 E[X] 是这一分布的数学期望。

常用一维随机变量的期望如下：

0 - 1 分布：

　　　　　　　　　　　　　　　　　　　　　　E[X] = p

二项分布， X ~ B(n, p)：

　　　　　　　　　　　　　　　　　　　　　　E[X] = np

泊松分布， X ~ P(λ)：

　　　　　　　　　　　　　　　　　　　　　　E[X] = λ

均匀分布， X ~ U(a, b)：

　　　　　　　　　　　　　　　　　　　　　　E[X] = (a + b) / 2

指数分布， X ~ E(λ)：

　　　　　　　　　　　　　　　　　　　　　　E[X] = 1 / λ

正态分布， X ~ N(μ, σ^2)：

　　　　　　　　　　　　　　　　　　　　　　E[X] = μ

以下推导泊松分布及均匀分布的期望：

泊松分布：

均匀分布：

举个栗子

随机变量的数字特征之数学期望

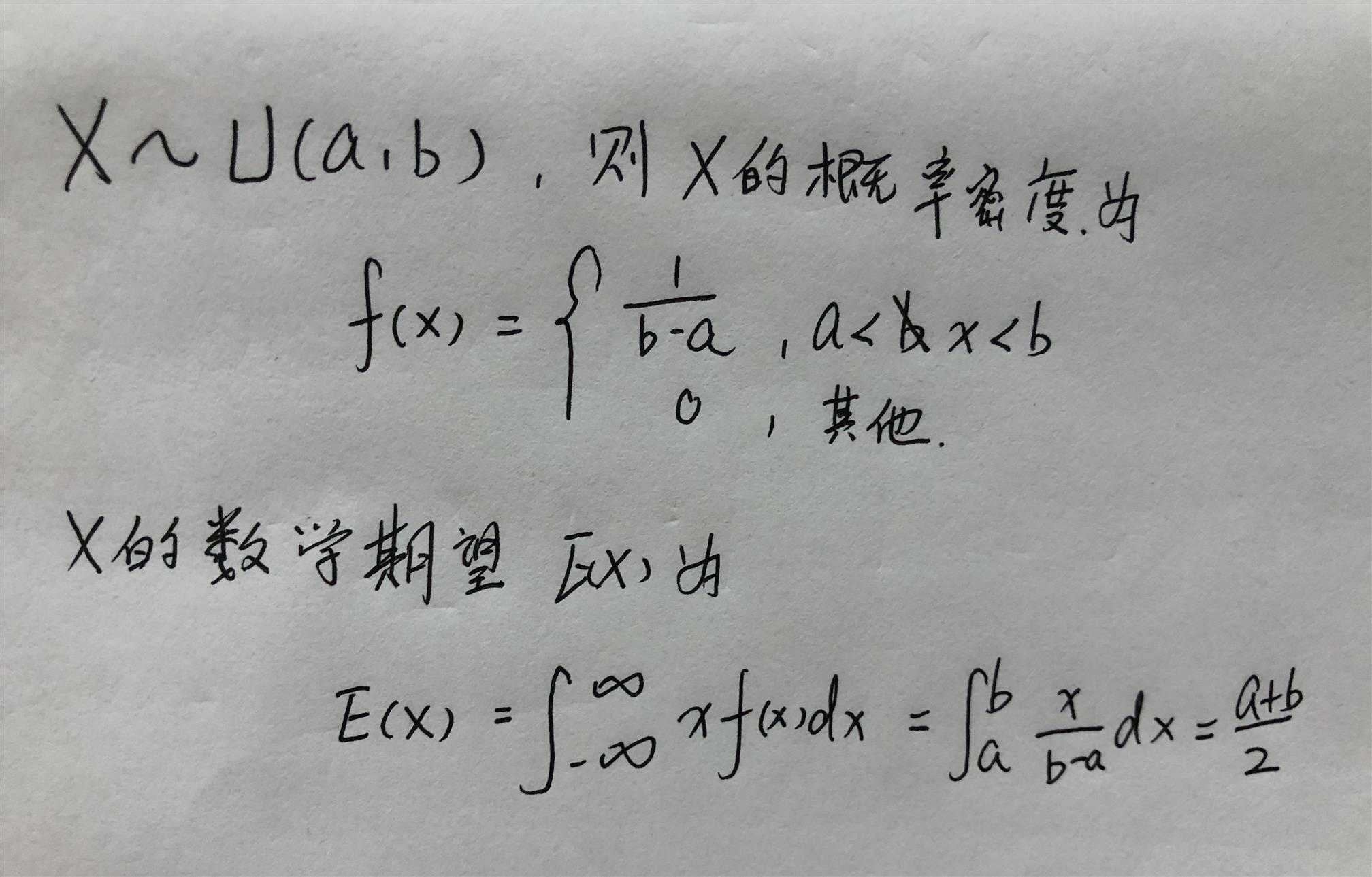
标签：重要   完全   img   权重   随机   函数   泊松分布   正是   数字   

原文地址：https://www.cnblogs.com/shenxi-ricardo/p/11588633.html