标签：属性 概念 size src 概率统计 工作 数据集 info com
一、决策树
决策树(decision tree)是一种基本的分类与回归方法。
决策树由结点(node)和有向边(directed edge)组成。
结点有两种类型：内部结点(internal node)和叶结点(leaf node)。
内部结点表示一个特征或属性，叶结点表示一个类。
1、决策树的构建：
特征选择、决策树的生成和决策树的修剪。
通常特征选择的标准是信息增益(information gain)或信息增益比。
信息增益：在划分数据集之前之后信息发生的变化成为信息增益。
2、香农熵
集合信息的度量方式成为香农熵或者简称为熵。
熵定义为信息的期望值。在信息论与概率统计中，熵是表示随机变量不确定性的度量。
如果待分类的事务可能划分在多个分类之中，则符号xi的信息定义为
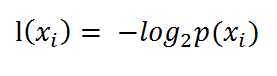其中p(xi)是选择该分类的概率。通过上式，我们可以得到所有类别的信息。
为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值(数学期望)，通过下面的公式得到：
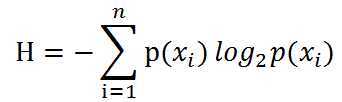
期中n是分类的数目。熵越大，随机变量的不确定性就越大。当熵中的概率由数据估计得到时，所对应的熵称为经验熵。
3、经验熵的计算和最优特征的选择
工作原理如下：得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。第一次划分之后，数据集被向下传递到树的分支的下一个结点。在这个结点上，我们可以再次划分数据。因此我们可以采用递归的原则处理数据集。
标签：属性 概念 size src 概率统计 工作 数据集 info com
原文地址：https://www.cnblogs.com/fd-682012/p/11593040.html
