标签:style blog http io color os ar for sp
Given an index k, return the kth row of the Pascal‘s triangle.
For example, given k = 3,
Return [1,3,3,1].
Note:
Could you optimize your algorithm to use only O(k) extra space?
首先我们来熟悉下杨辉三角形的特点:
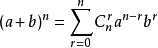
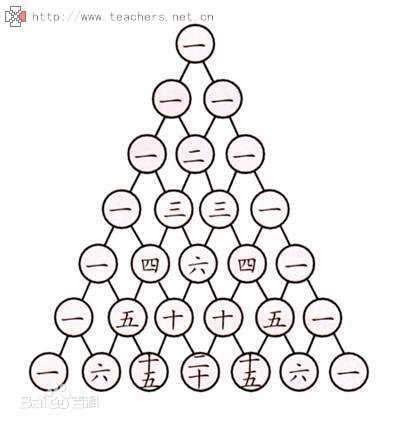
1.空间复杂度为O(k2)比较容易想到,代码如下,注意vector二维数组的初始化,必须定义二维数组的行数:
class Solution { public: vector<int> getRow(int rowIndex) { vector<vector<int>> vec(rowIndex+1); for(int i=0;i<=rowIndex;++i) { vec[i].push_back(1); for(int j=1;j<=i-1;++j) { vec[i].push_back(vec[i-1][j-1]+vec[i-1][j]); } if(i!=0) vec[i].push_back(1); } return vec[rowIndex]; } };
2.空间复杂度O(k),我们可以只用一个数组来表示杨辉三角形,当我们在某一行从前往后看的时候,发现最后一个加上倒数第二个等于下一行的最后一个,且不会更新我们需要的那个数,进而可以算出下一行的倒数第二个。
代码如下:
class Solution { public: vector<int> getRow(int rowIndex) { vector<int> vec(rowIndex+1,0); int i,j; for (i=0; i<=rowIndex; ++i) { if(i==0) vec[0]=1; else { for (j=i-1; j>=1; --j)
{ vec[j]=vec[j]+vec[j-1]; } vec[i]=1; } } return vec; } };
标签:style blog http io color os ar for sp
原文地址:http://www.cnblogs.com/fightformylife/p/4054545.html